Advertisements
Advertisements
Question
Tow godowns, A and B, have grain storage capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F, whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
| Transportation cost per quintal(in Rs.) | ||
| From-> | A | B |
| To | ||
| D | 6.00 | 4.00 |
| E | 3.00 | 2.00 |
| F | 2.50 | 3.00 |
How should the supplies be transported in order that the transportation cost is minimum?
Advertisements
Solution
Let godown A supply x quintals and y quintals of grain to the shops D and E respectively.
Then, (100 − x − y) will be supplied to shop F.
The requirement at shop D is 60 quintals since, x quintals are transported from godown A.
Therefore, the remaining (60 − x) quintals will be transported from godown B.
Similarly, (50 − y) quintals and 40 − (100 − x − y) i.e. (x + y − 60) quintals will be transported from godown B to shop E and F respectively.
The given problem can be represented diagrammatically as follows.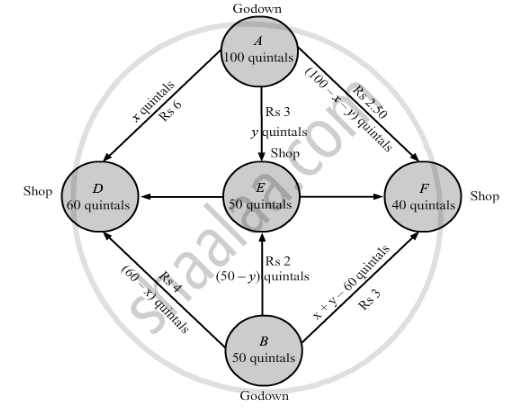
Quantity of the grain cannot be negative.Therefore,
x ≥ 0 , y ≥ 0 and 100 - x - y ≥ 0
⇒ x ≥ 0 , y ≥ 0 , and x + y ≤ 100
60 - x ≥ 0 , 50 - y ≥ 0 , and x + y - 60 ≥ 0
⇒ x ≤ 60 , y ≤ 50 , and x + y ≥ 60
Total transportation cost Z is given by,
\[Z = 6x + 3y + 2 . 5\left( 100 - x - y \right) + 4\left( 60 - x \right) + 2\left( 50 - y \right) + 3\left( x + y - 60 \right)\]
\[ = 6x + 3y + 250 - 2 . 5x - 2 . 5y + 240 - 4x + 100 - 2y + 3x + 3y - 180\]
\[ = 2 . 5x + 1 . 5y + 410\]
The given problem can be formulated as:
Minimize Z = 2.5x + 1.5y + 410
subject to the constraints,
\[x + y \leq 100\]
\[x \leq 60\]
\[y \leq 50\]
\[x + y \geq 60\]
\[x, y \geq 0\]
First we will convert inequations into equations as follows:
x + y = 100, x = 60, y = 50, x + y =60, x = 0 and y = 0
Region represented by x + y ≤ 100:
The line x + y = 100 meets the coordinate axes at A1(100, 0) and B1(0, 100) respectively. By joining these points we obtain the line x + y = 100. Clearly (0,0) satisfies the x + y = 100. So, the region which contains the origin represents the solution set of the inequation x + y ≤ 100.
Region represented by x ≤ 60:
x = 60 is the line that passes (60, 0) and is parallel to the Y axis.The region to the left of the line x = 60 will satisfy the inequation x ≤ 60.
Region represented by y ≤ 50:
y = 50 is the line that passes (0, 50) and is parallel to the X axis.The region below the line y = 50 will satisfy the inequation y ≤ 50.
Region represented by x + y ≥ 60:
The line x + y = 60 meets the coordinate axes at C1(60, 0) and \[D_1 \left( 0, 60 \right)\] respectively. By joining these points we obtain the line x + y = 60. Clearly (0,0) does not satisfies the inequation x + y ≥ 60. So,the region which does not contain the origin represents the solution set of the inequation x + y ≥ 60.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 100, x ≤ 60, y ≤ 50, x + y ≥ 60, x ≥ 0 and y ≥ 0 are as follows.
The corner points are C1(60, 0), G1(60, 40), F1(50, 50), and E1(10, 50).
The values of Z at these corner points are as follows.
| Corner point | Z = 2.5x + 1.5y + 410 |
| C1(60, 0) | 560 |
| G1(60, 40) | 620 |
| F1(50, 50) | 610 |
| E1(10, 50) | 510 |
The minimum value of Z is 510 at E1(10, 50).
Thus, the amount of grain transported from A to D, E, and F is 10 quintals, 50 quintals, and 40 quintals respectively and from B to D, E, and F is 50 quintals, 0 quintals, and 0 quintals respectively.
The minimum cost is Rs 510.
APPEARS IN
RELATED QUESTIONS
A dealer in rural area wishes to purchase a number of sewing machines. He has only Rs 5,760 to invest and has space for at most 20 items for storage. An electronic sewing machine cost him Rs 360 and a manually operated sewing machine Rs 240. He can sell an electronic sewing machine at a profit of Rs 22 and a manually operated sewing machine at a profit of Rs 18. Assuming that he can sell all the items that he can buy, how should he invest his money in order to maximize his profit? Make it as a LPP and solve it graphically.
Minimize :Z=6x+4y
Subject to : 3x+2y ≥12
x+y ≥5
0 ≤x ≤4
0 ≤ y ≤ 4
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs 7 profit and B at a profit of Rs 4. Find the production level per day for maximum profit graphically.
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30, respectively. The company makes a profit of Rs 80 on each piece of type A and Rs 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week?
Solve the following LPP by graphical method:
Maximize: z = 3x + 5y
Subject to: x + 4y ≤ 24
3x + y ≤ 21
x + y ≤ 9
x ≥ 0, y ≥ 0
Also find the maximum value of z.
Maximise Z = x + 2y subject to the constraints
`x + 2y >= 100`
`2x - y <= 0`
`2x + y <= 200`
Solve the above LPP graphically
Solve the following LPP by graphical method:
Minimize Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
A dietician wishes to mix two kinds ·of food X· and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B arid 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin.B | Vitamin C |
| X | 1 unit | 2 unit | 3 unit |
| Y | 2 unit | 2 unit | 1 unit |
Orie kg of food X costs Rs 24 and one kg of food Y costs Rs 36. Using Linear Programming, find the least cost of the total mixture. which will contain the required vitamins.
Solve the following LPP graphically :
Maximise Z = 105x + 90y
subject to the constraints
x + y ≤ 50
2x + y ≤ 80
x ≥ 0, y ≥ 0.
Maximize Z = 5x + 3y
Subject to
\[3x + 5y \leq 15\]
\[5x + 2y \leq 10\]
\[ x, y \geq 0\]
Maximize Z = 15x + 10y
Subject to
\[3x + 2y \leq 80\]
\[2x + 3y \leq 70\]
\[ x, y \geq 0\]
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1and F2 are available. Food F1 costs Rs 4 per unit and F2 costs Rs 6 per unit one unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem and find graphically the minimum cost for diet that consists of mixture of these foods and also meets the mineral nutritional requirements
Kellogg is a new cereal formed of a mixture of bran and rice that contains at least 88 grams of protein and at least 36 milligrams of iron. Knowing that bran contains 80 grams of protein and 40 milligrams of iron per kilogram, and that rice contains 100 grams of protein and 30 milligrams of iron per kilogram, find the minimum cost of producing this new cereal if bran costs Rs 5 per kg and rice costs Rs 4 per kg
A farmer mixes two brands P and Q of cattle feed. Brand P, costing ₹250 per bag, contains 2 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing ₹200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
A manufacturer of Furniture makes two products : chairs and tables. processing of these products is done on two machines A and B. A chair requires 2 hrs on machine A and 6 hrs on machine B. A table requires 4 hrs on machine A and 2 hrs on machine B. There are 16 hrs of time per day available on machine A and 30 hrs on machine B. Profit gained by the manufacturer from a chair and a table is Rs 3 and Rs 5 respectively. Find with the help of graph what should be the daily production of each of the two products so as to maximize his profit.
A firm manufactures two products A and B. Each product is processed on two machines M1 and M2. Product A requires 4 minutes of processing time on M1 and 8 min. on M2 ; product B requires 4 minutes on M1 and 4 min. on M2. The machine M1 is available for not more than 8 hrs 20 min. while machine M2 is available for 10 hrs. during any working day. The products A and B are sold at a profit of Rs 3 and Rs 4 respectively.
Formulate the problem as a linear programming problem and find how many products of each type should be produced by the firm each day in order to get maximum profit.
A manufacturer makes two products A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 of product A and 16 of product B. A working week consists of 40 hours of production and weekly turnover must not be less than Rs 10000. If the profit on each of product A is Rs 20 and on product B is Rs 30, then how many of each should be produced so that the profit is maximum. Also, find the maximum profit.
A manufacturer of patent medicines is preparing a production plan on medicines, A and B. There are sufficient raw materials available to make 20000 bottles of A and 40000 bottles of B, but there are only 45000 bottles into which either of the medicines can be put. Further, it takes 3 hours to prepare enough material to fill 1000 bottles of A, it takes 1 hour to prepare enough material to fill 1000 bottles of B and there are 66 hours available for this operation. The profit is Rs 8 per bottle for A and Rs 7 per bottle for B. How should the manufacturer schedule his production in order to maximize his profit?
A gardener has supply of fertilizer of type I which consists of 10% nitrogen and 6% phosphoric acid and type II fertilizer which consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, he finds that he needs at least 14 kg of nitrogen and 14 kg of phosphoric acid for his crop. If the type I fertilizer costs 60 paise per kg and type II fertilizer costs 40 paise per kg, determine how many kilograms of each fertilizer should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost?
A man owns a field of area 1000 sq.m. He wants to plant fruit trees in it. He has a sum of Rs 1400 to purchase young trees. He has the choice of two types of trees. Type A requires 10 sq.m of ground per tree and costs Rs 20 per tree and type B requires 20 sq.m of ground per tree and costs Rs 25 per tree. When fully grown, type A produces an average of 20 kg of fruit which can be sold at a profit of Rs 2.00 per kg and type B produces an average of 40 kg of fruit which can be sold at a profit of Rs. 1.50 per kg. How many of each type should be planted to achieve maximum profit when the trees are fully grown? What is the maximum profit?
A manufacturing company makes two models A and B of a product. Each piece of model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of model B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of ₹8000 on each piece of model A and ₹12000 on each piece of model B. How many pieces of model A and model B should be manufactured per week to realise a maximum profit? What is the maximum profit per week?
There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below:
| From \ To | Cost (in ₹) | ||
| A | B | C | |
| P | 160 | 100 | 150 |
| Q | 100 | 120 | 100 |
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost?
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Types of Toys | Machines | ||
| I | II | III | |
| A | 12 | 18 | 6 |
| B | 6 | 0 | 9 |
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at ₹7 profit and that of B at a profit of ₹4. Find the production level per day for maximum profit graphically.
Maximize: z = 3x + 5y Subject to
x +4y ≤ 24 3x + y ≤ 21
x + y ≤ 9 x ≥ 0 , y ≥0
A company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is ₹ 40 on each unit of the product of type A and ₹ 50 on each unit of type B. How many units of each type should the company manufacture so as to earn a maximum profit? Use linear programming to find the solution.
A company manufactures two types of cardigans: type A and type B. It costs ₹ 360 to make a type A cardigan and ₹ 120 to make a type B cardigan. The company can make at most 300 cardigans and spend at most ₹ 72000 a day. The number of cardigans of type B cannot exceed the number of cardigans of type A by more than 200. The company makes a profit of ₹ 100 for each cardigan of type A and ₹ 50 for every cardigan of type B.
Formulate this problem as a linear programming problem to maximize the profit to the company. Solve it graphically and find the maximum profit.
Find the graphical solution for the system of linear inequation 2x + y ≤ 2, x − y ≤ 1
The minimum value of z = 10x + 25y subject to 0 ≤ x ≤ 3, 0 ≤ y ≤ 3, x + y ≥ 5 is ______.
Area of the region bounded by y = cos x, x = 0, x = π and X-axis is ______ sq.units.
Z = 20x1 + 20x2, subject to x1 ≥ 0, x2 ≥ 0, x1 + 2x2 ≥ 8, 3x1 + 2x2 ≥ 15, 5x1 + 2x2 ≥ 20. The minimum value of Z occurs at ____________.
In Corner point method for solving a linear programming problem the first step is to ____________.
The corner points of the bounded feasible region of a LPP are A(0,50), B(20, 40), C(50, 100) and D(0, 200) and the objective function is Z = x + 2y. Then the maximum value is ____________.
The maximum value of Z = 3x + 4y subjected to contraints x + y ≤ 40, x + 2y ≤ 60, x ≥ 0 and y ≥ 0 is ____________.
Any point in the feasible region that gives the optional value (maximum or minimum) of the objective function is called:-
The corner points of the shaded unbounded feasible region of an LPP are (0, 4), (0.6, 1.6) and (3, 0) as shown in the figure. The minimum value of the objective function Z = 4x + 6y occurs at ______.
The shaded part of given figure indicates in feasible region, then the constraints are:
What is the result if no feasible region exists?
