Advertisements
Advertisements
Question
Solve the following linear programming problem graphically :
Maximise Z = 7x + 10y subject to the constraints
4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 10
x ≥ 0, y ≥ 0
Solution
The given constraints are 4x + 6y ≤ 240, 6x + 3y ≤ 240, x ≥ 10, x ≥ 0, y ≥ 0.
Firstly, convert the given inequations into equations, we obtain the following equations:
4x + 6y = 240, 6x + 3y = 240, x = 10, x = 0 and y = 0.
The line 4x + 6y = 240 meets the coordinate axes at A1(60, 0) and B1(0, 40), respectively. Join these points to obtain the line 4x + 6y = 240
Clearly (0,0) satisfies the inequation 4x + 6y ≤ 240. So, the region containing the origin represents the solution set of the inequation 4x + 6y ≤ 240.
The line 6x + 3y = 240 meets the coordinate axes at A2(40, 0) and B2(0, 80), respectively. Join these points to obtain the line 6x + 3y = 240.
Clearly (0,0) satisfies the inequation 6x + 3y ≤ 240. So, the region containing the origin represents the solution set of the inequation 6x + 3y ≤ 240.
The line x = 10 is the line that passes through A3(10, 0) and parallel to y-axis.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The feasible region determined by the system of constraints is shown below:
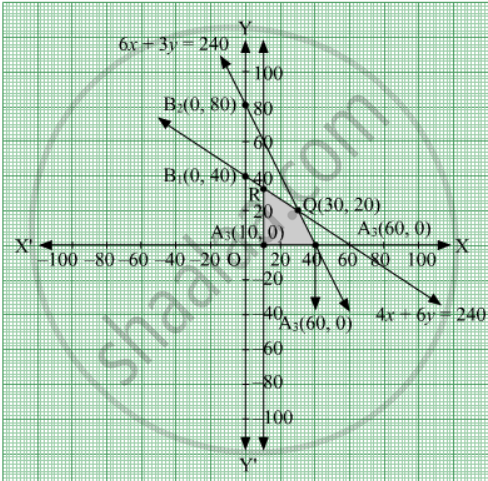
The corner points of the feasible region are A3(10, 0), A2(40, 0), Q(30, 20) and R (20, `80/3`)
The values of Z at these corner points are as follows:
| Corner point | Value of the objective function Z = 7x + 10y |
| A3(10, 0) | Z = 7 × 10 + 10 × 0 = 70 |
| A2(40, 0) | Z = 7 × 40 + 10 × 0 = 280 |
| Q(30, 20) | Z = 7 × 30 + 10 × 20 = 410 (Maximum) |
| R(20, 80/3) | `Z = 7 xx 20 + xx 80/3 = 1220/3` |
Thus, the maximum value of the objective function Z is 410 which is obtained at x = 30 and y = 20.
APPEARS IN
RELATED QUESTIONS
Solve the following L.P.P. graphically Maximise Z = 4x + y
Subject to following constraints x + y ≤ 50
3x + y ≤ 90,
x ≥ 10
x, y ≥ 0
Solve the following LPP graphically :
Maximise Z = 105x + 90y
subject to the constraints
x + y ≤ 50
2x + y ≤ 80
x ≥ 0, y ≥ 0.
Maximise z = 8x + 9y subject to the constraints given below :
2x + 3y ≤ 6
3x − 2y ≤6
y ≤ 1
x, y ≥ 0
Minimize Z = 3x1 + 5x2
Subject to
\[x_1 + 3 x_2 \geq 3\]
\[ x_1 + x_2 \geq 2\]
\[ x_1 , x_2 \geq 0\]
Find the maximum and minimum value of 2x + y subject to the constraints:
x + 3y ≥ 6, x − 3y ≤ 3, 3x + 4y ≤ 24, − 3x + 2y ≤ 6, 5x + y ≥ 5, x, y ≥ 0.
A firm manufactures two products A and B. Each product is processed on two machines M1 and M2. Product A requires 4 minutes of processing time on M1 and 8 min. on M2 ; product B requires 4 minutes on M1 and 4 min. on M2. The machine M1 is available for not more than 8 hrs 20 min. while machine M2 is available for 10 hrs. during any working day. The products A and B are sold at a profit of Rs 3 and Rs 4 respectively.
Formulate the problem as a linear programming problem and find how many products of each type should be produced by the firm each day in order to get maximum profit.
A firm manufacturing two types of electric items, A and B, can make a profit of Rs 20 per unit of A and Rs 30 per unit of B. Each unit of A requires 3 motors and 4 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of these per month is restricted to 210 motors and 300 transformers. Type B is an export model requiring a voltage stabilizer which has a supply restricted to 65 units per month. Formulate the linear programing problem for maximum profit and solve it graphically.
A firm manufactures headache pills in two sizes A and B. Size A contains 2 grains of aspirin, 5 grains of bicarbonate and 1 grain of codeine; size B contains 1 grain of aspirin, 8 grains of bicarbonate and 66 grains of codeine. It has been found by users that it requires at least 12 grains of aspirin, 7.4 grains of bicarbonate and 24 grains of codeine for providing immediate effects. Determine graphically the least number of pills a patient should have to get immediate relief. Determine also the quantity of codeine consumed by patient.
A manufacturer produces two types of steel trunks. He has two machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively. How many trunks of each type must he make each day to make maximum profit?
A manufacturing company makes two models A and B of a product. Each piece of model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of model B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of ₹8000 on each piece of model A and ₹12000 on each piece of model B. How many pieces of model A and model B should be manufactured per week to realise a maximum profit? What is the maximum profit per week?
There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below:
| From \ To | Cost (in ₹) | ||
| A | B | C | |
| P | 160 | 100 | 150 |
| Q | 100 | 120 | 100 |
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost?
An aeroplane can carry a maximum of 200 passengers. A profit of ₹1000 is made on each executive class ticket and a profit of ₹600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However, atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit of the airline. What is the maximum profit?
Tow godowns, A and B, have grain storage capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F, whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
| Transportation cost per quintal(in Rs.) | ||
| From-> | A | B |
| To | ||
| D | 6.00 | 4.00 |
| E | 3.00 | 2.00 |
| F | 2.50 | 3.00 |
How should the supplies be transported in order that the transportation cost is minimum?
A medical company has factories at two places, A and B. From these places, supply is made to each of its three agencies situated at P, Q and R. The monthly requirements of the agencies are respectively 40, 40 and 50 packets of the medicines, while the production capacity of the factories, A and B, are 60 and 70 packets respectively. The transportation cost per packet from the factories to the agencies are given below:
| Transportation Cost per packet(in Rs.) | ||
| From-> | A | B |
| To | ||
| P | 5 | 4 |
| Q | 4 | 2 |
| R | 3 | 5 |
A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is used to product A and product B. Each unit of product A requires 2, 1 and 1 running feet and each unit of product B requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If product A is sold for Rs. 48 per unit and product B is sold for Rs. 40 per unit, how many units of product A and product B should be produced and sold by the carpenter, in order to obtain the maximum gross income? Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible region in the graph.
Maximum value of 4x + 13y subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is ______.
The minimum value of z = 2x + 9y subject to constraints x + y ≥ 1, 2x + 3y ≤ 6, x ≥ 0, y ≥ 0 is ______.
For the function z = 19x + 9y to be maximum under the constraints 2x + 3y ≤ 134, x + 5y ≤ 200, x ≥ 0, y ≥ 0; the values of x and y are ______.
If 4x + 5y ≤ 20, x + y ≥ 3, x ≥ 0, y ≥ 0, maximum 2x + 3y is ______.
Of all the points of the feasible region for maximum or minimum of objective function the points.
A set of values of decision variables which satisfies the linear constraints and nn-negativity conditions of an L.P.P. is called its ____________.
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and ____________.
Solve the following Linear Programming Problem graphically:
Maximize Z = 400x + 300y subject to x + y ≤ 200, x ≤ 40, x ≥ 20, y ≥ 0
The constraints –x1 + x2 ≤ 1, –x1 + 3x2 ≤ 9, x1x2 ≥ 0 define on ______.
The shaded part of given figure indicates in feasible region, then the constraints are:

The objective function Z = x1 + x2, subject to the constraints are x1 + x2 ≤ 10, – 2x1 + 3x2 ≤ 15, x1 ≤ 6, x1, x2 ≥ 0, has maximum value ______ of the feasible region.
Solve the following linear programming problem graphically:
Minimize: Z = 5x + 10y
Subject to constraints:
x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0.
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
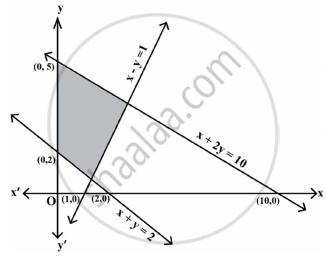
Which of the following is not a constraint to the given Linear Programming Problem?
Find feasible solution for the following system of linear inequation graphically.
3x + 4y ≥ 12, 4x + 7y ≤ 28, x ≥ 0, y ≥ 0
