Advertisements
Advertisements
Question
A manufacturing company makes two models A and B of a product. Each piece of model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of model B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of ₹8000 on each piece of model A and ₹12000 on each piece of model B. How many pieces of model A and model B should be manufactured per week to realise a maximum profit? What is the maximum profit per week?
Solution
Suppose x pieces of model A and y pieces of model B are manufactured per week.
Since each piece of model A requires 9 labour hours and each piece of model B requires 12 labour hours for fabricating, therefore, x pieces of model A and y pieces of model B require (9x + 12y) labour hours for fabricating. But, the maximum labour hours available for fabricating are 180.
∴ 9x + 12y ≤ 180
⇒ 3x + 4y ≤ 60
Similarly, each piece of model A requires 1 labour hour and each piece of model B requires 3 labour hours for finishing, therefore, x pieces of model A and y pieces of model B require (x + 3y) labour hours for finishing. But, the maximum labour hours available for finishing are 30.
∴ x + 3y ≤ 30
The profit from each piece of model A is ₹8,000 and from each piece of model B is ₹12,000. Therefore, the total profit from x pieces of model A and y pieces of model B is ₹(8,000x + 12,000y).
Thus, the given linear programming problem is
Maximise Z = 8000x + 12000y
subject to the constraints
3x + 4y ≤ 60
x + 3y ≤ 30
x, y ≥ 0
The feasible region determined by the given constraints can be diagrammatically represented as,
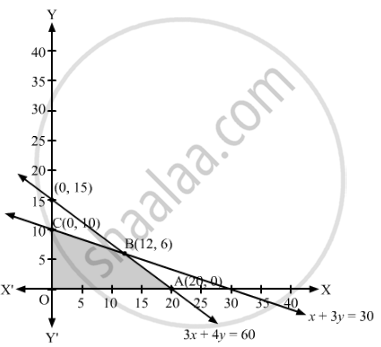
The coordinates of the corner points of the feasible region are O(0, 0), A(20, 0), B(12, 6) and C(0, 10).
The value of the objective function at these points are given in the following table.
| Corner Point | Z = 8000x + 12000y |
| (0, 0) | 8000 × 0 + 12000 × 0 = 0 |
| (20, 0) | 8000 × 20 + 12000 × 0 = 160000 |
| (12, 6) | 8000 × 12 + 12000 × 6 = 168000 → Maximum |
| (0, 10) | 8000 × 0 + 12000 × 10 = 120000 |
The maximum value of Z is 168000 at x = 12, y = 6.
Hence, the manufacturing company should produce 12 pieces of model A and 6 pieces of model B to realise maximum profit. The maximum profit is ₹1,68,000.
APPEARS IN
RELATED QUESTIONS
Minimize `z=4x+5y ` subject to `2x+y>=7, 2x+3y<=15, x<=3,x>=0, y>=0` solve using graphical method.
A cooperative society of farmers has 50 hectares of land to grow two crops A and B. The profits from crops A and B per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be used for crops A and B at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. Keeping in mind that the protection of fish and other wildlife is more important than earning profit, how much land should be allocated to each crop so as to maximize the total profit? Form an LPP from the above and solve it graphically. Do you agree with the message that the protection of wildlife is utmost necessary to preserve the balance in environment?
Minimize :Z=6x+4y
Subject to : 3x+2y ≥12
x+y ≥5
0 ≤x ≤4
0 ≤ y ≤ 4
Solve the following L.P.P. graphically Maximise Z = 4x + y
Subject to following constraints x + y ≤ 50
3x + y ≤ 90,
x ≥ 10
x, y ≥ 0
Maximise z = 8x + 9y subject to the constraints given below :
2x + 3y ≤ 6
3x − 2y ≤6
y ≤ 1
x, y ≥ 0
Maximize Z = 5x + 3y
Subject to
\[3x + 5y \leq 15\]
\[5x + 2y \leq 10\]
\[ x, y \geq 0\]
Maximize Z = 4x + 3y
Subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Maximize Z = x + y
Subject to
\[- 2x + y \leq 1\]
\[ x \leq 2\]
\[ x + y \leq 3\]
\[ x, y \geq 0\]
Solved the following linear programming problem graphically:
Maximize Z = 60x + 15y
Subject to constraints
\[x + y \leq 50\]
\[3x + y \leq 90\]
\[ x, y \geq 0\]
Solve the following LPP graphically:
Maximize Z = 20 x + 10 y
Subject to the following constraints
\[x +\]2\[y \leq\]28
3x+ \[y \leq\]24
\[x \geq\] 2x.
\[y \geq\] 0
A diet of two foods F1 and F2 contains nutrients thiamine, phosphorous and iron. The amount of each nutrient in each of the food (in milligrams per 25 gms) is given in the following table:
Nutrients |
Food |
F1 | F2 |
| Thiamine | 0.25 | 0.10 |
|
| Phosphorous | 0.75 | 1.50 | |
| Iron | 1.60 | 0.80 | |
The minimum requirement of the nutrients in the diet are 1.00 mg of thiamine, 7.50 mg of phosphorous and 10.00 mg of iron. The cost of F1 is 20 paise per 25 gms while the cost of F2 is 15 paise per 25 gms. Find the minimum cost of diet.
One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no storage of the other ingredients used in making the cakes.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing ₹250 per bag, contains 2 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing ₹200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 gm of silver and 1 gm of gold while that of type B requires 1 gm of silver and 2 gm of gold. The company can produce 9 gm of silver and 8 gm of gold. If each unit of type A brings a profit of Rs 40 and that of type B Rs 50, find the number of units of each type that the company should produce to maximize the profit. What is the maximum profit?
A firm manufacturing two types of electric items, A and B, can make a profit of Rs 20 per unit of A and Rs 30 per unit of B. Each unit of A requires 3 motors and 4 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of these per month is restricted to 210 motors and 300 transformers. Type B is an export model requiring a voltage stabilizer which has a supply restricted to 65 units per month. Formulate the linear programing problem for maximum profit and solve it graphically.
A factory uses three different resources for the manufacture of two different products, 20 units of the resources A, 12 units of B and 16 units of C being available. 1 unit of the first product requires 2, 2 and 4 units of the respective resources and 1 unit of the second product requires 4, 2 and 0 units of respective resources. It is known that the first product gives a profit of 2 monetary units per unit and the second 3. Formulate the linear programming problem. How many units of each product should be manufactured for maximizing the profit? Solve it graphically.
A manufacturer produces two types of steel trunks. He has two machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively. How many trunks of each type must he make each day to make maximum profit?
A producer has 30 and 17 units of labour and capital respectively which he can use to produce two type of goods x and y. To produce one unit of x, 2 units of labour and 3 units of capital are required. Similarly, 3 units of labour and 1 unit of capital is required to produce one unit of y. If x and y are priced at Rs 100 and Rs 120 per unit respectively, how should be producer use his resources to maximize the total revenue? Solve the problem graphically.
If a young man drives his vehicle at 25 km/hr, he has to spend ₹2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to ₹5 per km. He has ₹100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
A library has to accommodate two different types of books on a shelf. The books are 6 cm and 4 cm thick and weigh 1 kg and \[1\frac{1}{2}\] kg each respectively. The shelf is 96 cm long and atmost can support a weight of 21 kg. How should the shelf be filled with the books of two types in order to include the greatest number of books? Make it as an LPP and solve it graphically.
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time. If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the number of tennis rackets and cricket bats that the factory must manufacture to earn the maximum profit. Make it as an LPP and solve it graphically.
A cooperative society of farmers has 50 hectares of land to grow two crops X and Y. The profits from crops X and Y per hectare are estimated as ₹10,500 and ₹9,000 respectively. To control weeds, a liquid herbicide has to be used for crops X and Y at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. How much land should be allocated to each crop so as to maximise the total profit of the society?
A manufacturer has three machine I, II, III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine III must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the use of all the three machines.
The number of hours required for producing 1 unit each of M and N on the three machines are given in the following table:
| Items | Number of hours required on machines | ||
| I | II | III | |
| M | 1 | 2 | 1 |
| N | 2 | 1 | 1.25 |
She makes a profit of ₹600 and ₹400 on items M and N respectively. How many of each item should she produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?
There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below:
| From \ To | Cost (in ₹) | ||
| A | B | C | |
| P | 160 | 100 | 150 |
| Q | 100 | 120 | 100 |
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost?
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at ₹7 profit and that of B at a profit of ₹4. Find the production level per day for maximum profit graphically.
Find the solution set of inequalities 0 ≤ x ≤ 5, 0 ≤ 2y ≤ 7
The maximum value of Z = 5x + 4y, Subject to y ≤ 2x, x ≤ 2y, x + y ≤ 3, x ≥ 0, y ≥ 0 is ______.
The minimum value of z = 2x + 9y subject to constraints x + y ≥ 1, 2x + 3y ≤ 6, x ≥ 0, y ≥ 0 is ______.
If 4x + 5y ≤ 20, x + y ≥ 3, x ≥ 0, y ≥ 0, maximum 2x + 3y is ______.
In linear programming feasible region (or solution region) for the problem is ____________.
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities,
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and ____________.
In Corner point method for solving a linear programming problem the first step is to ____________.
A manufacturer wishes to produce two commodities A and B. The number of units of material, labour and equipment needed to produce one unit of each commodity is shown in the table given below. Also shown is the available number of units of each item, material, labour, and equipment.
| Items | Commodity A | Commodity B | Available no. of Units |
| Material | 1 | 2 | 8 |
| Labour | 3 | 2 | 12 |
| Equipment | 1 | 1 | 10 |
Find the maximum profit if each unit of commodity A earns a profit of ₹ 2 and each unit of B earns a profit of ₹ 3.
Any point in the feasible region that gives the optional value (maximum or minimum) of the objective function is called:-
Solve the following Linear Programming problem graphically:
Maximize: Z = 3x + 3.5y
Subject to constraints:
x + 2y ≥ 240,
3x + 1.5y ≥ 270,
1.5x + 2y ≤ 310,
x ≥ 0, y ≥ 0.
Find feasible solution for the following system of linear inequation graphically.
3x + 4y ≥ 12, 4x + 7y ≤ 28, x ≥ 0, y ≥ 0
