Question

A producer has 30 and 17 units of labour and capital respectively which he can use to produce two type of goods x and y. To produce one unit of x, 2 units of labour and 3 units of capital are required. Similarly, 3 units of labour and 1 unit of capital is required to produce one unit of y. If x and y are priced at Rs 100 and Rs 120 per unit respectively, how should be producer use his resources to maximize the total revenue? Solve the problem graphically.

Answer 1

Let \[x_1\] and \[y_1\] units of goods x and y were produced respectively.
Number of units of goods cannot be negative.
Therefore,\[x_1 , y_1 \geq 0\]
To produce one unit of x, 2 units of labour and for one unit of y, 3 units of labour are required \[2 x_1 + 3 y_1 \leq 30\]
To produce one unit of x, 3 units of capital is required and 1 unit of capital is required to produce one unit of y 
 \[3 x_1 + y_1 \leq 17\]

If x and y are priced at Rs 100 and Rs 120 per unit respectively, Therefore, cost of x₁ and y₁ units of goods x and y is Rs 100x₁ and Rs 120y₁ respectively.
Total revenue = Z = \[100 x_1 + 120 y_1\] which is to be maximised.

Thus, the mathematical formulat​ion of the given linear programmimg problem is 
Max Z =  \[100 x_1 + 120 y_1\]

subject to 

\[2 x_1 + 3 y_1 \leq 30\]
\[3 x_1 + y_1 \leq 17\]

\[x, y \geq 0\]

First we will convert inequations into equations as follows:
2x₁ + 3y₁ = 30, 3x₁ + y₁ = 17, x = 0 and y = 0

Region represented by 2x₁ + 3y₁ ≤ 30:
The line 2x₁ + 3y₁ = 30 meets the coordinate axes at A(15, 0) and B(0, 10) respectively. By joining these points we obtain the line
2x₁ + 3y₁ = 30. Clearly (0,0) satisfies the 2x₁ + 3y₁ = 30. So, the region which contains the origin represents the solution set of the inequation 2x₁ + 3y₁ ≤ 30.

Region represented by 3x₁ + y₁ ≤ 17:
The line 3x₁ + y₁ = 17 meets the coordinate axes at

\[C\left( \frac{17}{3}, 0 \right)\] and \[D\left( 0, 17 \right)\] respectively. By joining these points we obtain the line
3x₁ + y₁ = 17. Clearly (0,0) satisfies the inequation 3x₁ + y₁ ≤ 17. So,the region which contains the origin represents the solution set of the inequation 3x₁ + y₁ ≤ 17.

Region represented by x₁ ≥ 0 and y₁ ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.

The feasible region determined by the system of constraints 2x₁ + 3y₁ ≤ 30, 3x₁ + y₁ ≤ 17, x ≥ 0 and y ≥ 0 are as follows.

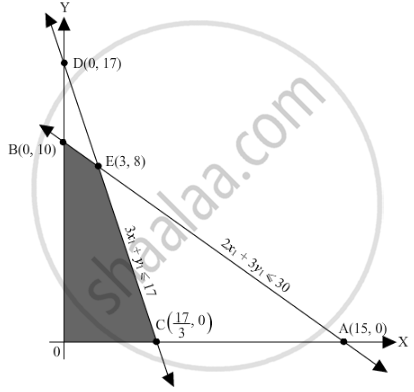
The corner points are B(0, 10), E(3, 8)  and  \[C\left( \frac{17}{3}, 0 \right)\]

The values of Z at these corner points

orner point	Z=  \[100 x_1 + 120 y_1\]
B	1200
E	1260
C	\[\frac{1700}{3}\]

The maximum value of Z is 1260 which is attained at E(3, 8).
Thus, the maximum revenue is Rs 1260 obtained when 3 units of x and 8 units of y were produced.are as follows