Advertisements
Advertisements
Question
Solve the following Linear Programming problem graphically:
Maximize: Z = 3x + 3.5y
Subject to constraints:
x + 2y ≥ 240,
3x + 1.5y ≥ 270,
1.5x + 2y ≤ 310,
x ≥ 0, y ≥ 0.
Solution
Changing inequations to equations
x + 2y = 240
3x + 1.5y = 270
1.5x + 2y = 310
For equation (i)
| x | 0 | 240 |
| y | 120 | 0 |
For equation (ii)
| x | 0 | 90 |
| y | 180 | 0 |
For equation (iii)
| x | 0 | 206.7 |
| y | 155 | 0 |
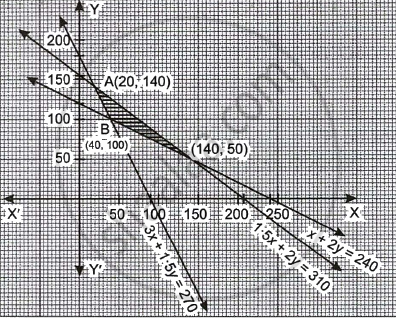
For A:
(3x + 1.5y = 270) × 2
(1.5x + 2y = 310) × 3/2
`\implies` 6x + 3y = 540
2.25x + 3y = 465
– – –
3.75x = 75
x = `75/3.75` = 20
y = `(310 - (1.5 xx 20))/2`
= `(310 - 30)/2`
= 140
A = (20, 140)
For B:
3x + 1.5y = 270
(x + 2y = 240) × 3
`\implies` 3x + 1.5y = 270
3x + 6y = 720
– – –
– 4.5y = – 450
`\implies` y = 100
x = 40
B = (40, 100)
For C:
x + 2y = 240
1.5x + 2y = 310
– – –
– 0.5x = – 70
x = 140
y = 50
C = (140, 50)
| Corner points | Max. Z = 3x + 3.5y |
| A(20, 140) | (3 × 20) + (3.5 × 140) = 550 |
| B(40, 100) | (3 × 40) + (3.5 × 100) = 470 |
| C(140, 50) | (3 × 140) + (50 × 3.5) = 595 `rightarrow` Max. |
Maximum value is 595 at (140, 50).
APPEARS IN
RELATED QUESTIONS
A dealer in rural area wishes to purchase a number of sewing machines. He has only Rs 5,760 to invest and has space for at most 20 items for storage. An electronic sewing machine cost him Rs 360 and a manually operated sewing machine Rs 240. He can sell an electronic sewing machine at a profit of Rs 22 and a manually operated sewing machine at a profit of Rs 18. Assuming that he can sell all the items that he can buy, how should he invest his money in order to maximize his profit? Make it as a LPP and solve it graphically.
A company manufactures bicycles and tricycles each of which must be processed through machines A and B. Machine A has maximum of 120 hours available and machine B has maximum of 180 hours available. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B.
If profits are Rs. 180 for a bicycle and Rs. 220 for a tricycle, formulate and solve the L.P.P. to determine the number of bicycles and tricycles that should be manufactured in order to maximize the profit.
Solve the following LPP by graphical method:
Maximize: z = 3x + 5y
Subject to: x + 4y ≤ 24
3x + y ≤ 21
x + y ≤ 9
x ≥ 0, y ≥ 0
Maximize Z = 9x + 3y
Subject to
\[2x + 3y \leq 13\]
\[ 3x + y \leq 5\]
\[ x, y \geq 0\]
Minimize Z = 18x + 10y
Subject to
\[4x + y \geq 20\]
\[2x + 3y \geq 30\]
\[ x, y \geq 0\]
Maximize Z = 10x + 6y
Subject to
\[3x + y \leq 12\]
\[2x + 5y \leq 34\]
\[ x, y \geq 0\]
Minimize Z = 2x + 4y
Subject to
\[x + y \geq 8\]
\[x + 4y \geq 12\]
\[x \geq 3, y \geq 2\]
Maximize Z = 3x + 5y
Subject to
\[x + 2y \leq 20\]
\[x + y \leq 15\]
\[ y \leq 5\]
\[ x, y \geq 0\]
Maximize Z = 3x + 3y, if possible,
Subject to the constraints
\[x - y \leq 1\]
\[x + y \geq 3\]
\[ x, y \geq 0\]
A factory owner purchases two types of machines, A and B, for his factory. The requirements and limitations for the machines are as follows:
| Area occupied by the machine |
Labour force for each machine |
Daily output in units |
|
| Machine A Machine B |
1000 sq. m 1200 sq. m |
12 men 8 men |
60 40 |
He has an area of 7600 sq. m available and 72 skilled men who can operate the machines.
How many machines of each type should he buy to maximize the daily output?
A firm manufacturing two types of electric items, A and B, can make a profit of Rs 20 per unit of A and Rs 30 per unit of B. Each unit of A requires 3 motors and 4 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of these per month is restricted to 210 motors and 300 transformers. Type B is an export model requiring a voltage stabilizer which has a supply restricted to 65 units per month. Formulate the linear programing problem for maximum profit and solve it graphically.
A chemical company produces two compounds, A and B. The following table gives the units of ingredients, C and D per kg of compounds A and B as well as minimum requirements of C and D and costs per kg of A and B. Find the quantities of A and B which would give a supply of C and D at a minimum cost.
| Compound | Minimum requirement | ||
| A | B | ||
| Ingredient C Ingredient D |
1 3 |
2 1 |
80 75 |
| Cost (in Rs) per kg | 4 | 6 | - |
A manufacturer makes two products A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 of product A and 16 of product B. A working week consists of 40 hours of production and weekly turnover must not be less than Rs 10000. If the profit on each of product A is Rs 20 and on product B is Rs 30, then how many of each should be produced so that the profit is maximum. Also, find the maximum profit.
A manufacturer produces two types of steel trunks. He has two machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively. How many trunks of each type must he make each day to make maximum profit?
An aeroplane can carry a maximum of 200 passengers. A profit of Rs 400 is made on each first class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats of first class. However, at least 4 times as many passengers prefer to travel by economy class to the first class. Determine how many each type of tickets must be sold in order to maximize the profit for the airline. What is the maximum profit.
A producer has 30 and 17 units of labour and capital respectively which he can use to produce two type of goods x and y. To produce one unit of x, 2 units of labour and 3 units of capital are required. Similarly, 3 units of labour and 1 unit of capital is required to produce one unit of y. If x and y are priced at Rs 100 and Rs 120 per unit respectively, how should be producer use his resources to maximize the total revenue? Solve the problem graphically.
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time. If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the number of tennis rackets and cricket bats that the factory must manufacture to earn the maximum profit. Make it as an LPP and solve it graphically.
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000. Make an LPP and solve it graphically.
The region represented by the inequation system x, y ≥ 0, y ≤ 6, x + y ≤ 3 is
Draw the graph of inequalities x ≤ 6, y −2 ≤ 0, x ≥ 0, y ≥ 0 and indicate the feasible region
Maximum value of 4x + 13y subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is ______.
The feasible region of an LPP is shown in the figure. If z = 3x + 9y, then the minimum value of z occurs at ______.
Of all the points of the feasible region for maximum or minimum of objective function the points.
In linear programming feasible region (or solution region) for the problem is ____________.
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities,
The feasible region (shaded) for a L.P.P is shown in the figure. The maximum Z = 5x + 7y is ____________.
Any point in the feasible region that gives the optional value (maximum or minimum) of the objective function is called:-
The objective function Z = ax + by of an LPP has maximum vaiue 42 at (4, 6) and minimum value 19 at (3, 2). Which of the following is true?
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
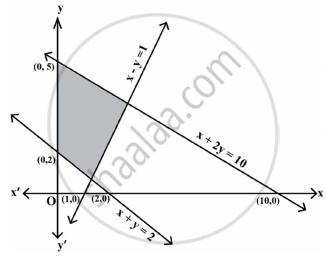
Which of the following is not a constraint to the given Linear Programming Problem?
