Advertisements
Advertisements
प्रश्न
Solve the following Linear Programming Problem graphically:
Maximize: z = – x + 2y,
Subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
उत्तर
The feasible region determined by the constraints, x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0 is given below.
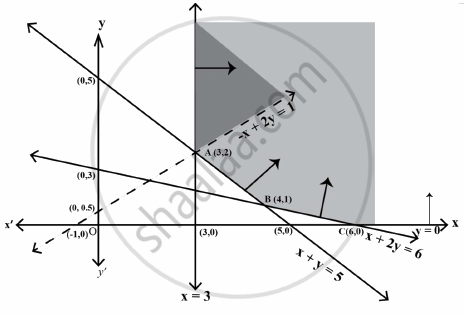
Here, it be seen the can that feasible region is unbounded.
The values of Z at corner points A (3, 2), B (4, 1) and C (6, 0) are given below.
| Corner point | Corresponding value of Z = – x + 2y |
| A (3, 2) | 1 ( may or may not be the maximum value) |
| B (4, 1) | –2 |
| C (6, 0) | –6 |
Since the feasible region is unbounded, Z = 1 may or may not be the maximum value.
Now, we draw the graph of the inequality, – x + 2y > 1, and we check whether the resulting open half-plane has any point/s, in common with the feasible region or not.
Here, the resulting open half plane has points in common with the feasible region.
Hence, Z = 1 is not the maximum value. We conclude, Z has no maximum value.
APPEARS IN
संबंधित प्रश्न
Solve the following LPP by using graphical method.
Maximize : Z = 6x + 4y
Subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
Also find maximum value of Z.
Find graphically, the maximum value of z = 2x + 5y, subject to constraints given below :
2x + 4y ≤ 83
x + y ≤ 6
x + y ≤ 4
x ≥ 0, y≥ 0
Solve the following L.P.P. graphically Maximise Z = 4x + y
Subject to following constraints x + y ≤ 50
3x + y ≤ 90,
x ≥ 10
x, y ≥ 0
Solve the following LPP by graphical method:
Minimize Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
Maximise z = 8x + 9y subject to the constraints given below :
2x + 3y ≤ 6
3x − 2y ≤6
y ≤ 1
x, y ≥ 0
Maximize Z = 5x + 3y
Subject to
\[3x + 5y \leq 15\]
\[5x + 2y \leq 10\]
\[ x, y \geq 0\]
Maximize Z = 9x + 3y
Subject to
\[2x + 3y \leq 13\]
\[ 3x + y \leq 5\]
\[ x, y \geq 0\]
Maximize Z = 50x + 30y
Subject to
\[2x + y \leq 18\]
\[3x + 2y \leq 34\]
\[ x, y \geq 0\]
Maximize Z = 4x + 3y
Subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Maximize Z = 2x + 3y
Subject to
\[x + y \geq 1\]
\[10x + y \geq 5\]
\[x + 10y \geq 1\]
\[ x, y \geq 0\]
Kellogg is a new cereal formed of a mixture of bran and rice that contains at least 88 grams of protein and at least 36 milligrams of iron. Knowing that bran contains 80 grams of protein and 40 milligrams of iron per kilogram, and that rice contains 100 grams of protein and 30 milligrams of iron per kilogram, find the minimum cost of producing this new cereal if bran costs Rs 5 per kg and rice costs Rs 4 per kg
One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no storage of the other ingredients used in making the cakes.
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
One kg of food X costs ₹16 and one kg of food Y costs ₹20. Find the least cost of the mixture which will produce the required diet?
Two tailors, A and B earn Rs 15 and Rs 20 per day respectively. A can stitch 6 shirts and 4 pants while B can stitch 10 shirts and 4 pants per day. How many days shall each work if it is desired to produce (at least) 60 shirts and 32 pants at a minimum labour cost?
A manufacturer of Furniture makes two products : chairs and tables. processing of these products is done on two machines A and B. A chair requires 2 hrs on machine A and 6 hrs on machine B. A table requires 4 hrs on machine A and 2 hrs on machine B. There are 16 hrs of time per day available on machine A and 30 hrs on machine B. Profit gained by the manufacturer from a chair and a table is Rs 3 and Rs 5 respectively. Find with the help of graph what should be the daily production of each of the two products so as to maximize his profit.
A furniture manufacturing company plans to make two products : chairs and tables. From its available resources which consists of 400 square feet to teak wood and 450 man hours. It is known that to make a chair requires 5 square feet of wood and 10 man-hours and yields a profit of Rs 45, while each table uses 20 square feet of wood and 25 man-hours and yields a profit of Rs 80. How many items of each product should be produced by the company so that the profit is maximum?
A firm manufactures headache pills in two sizes A and B. Size A contains 2 grains of aspirin, 5 grains of bicarbonate and 1 grain of codeine; size B contains 1 grain of aspirin, 8 grains of bicarbonate and 66 grains of codeine. It has been found by users that it requires at least 12 grains of aspirin, 7.4 grains of bicarbonate and 24 grains of codeine for providing immediate effects. Determine graphically the least number of pills a patient should have to get immediate relief. Determine also the quantity of codeine consumed by patient.
A manufacturer makes two products A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 of product A and 16 of product B. A working week consists of 40 hours of production and weekly turnover must not be less than Rs 10000. If the profit on each of product A is Rs 20 and on product B is Rs 30, then how many of each should be produced so that the profit is maximum. Also, find the maximum profit.
A firm manufactures two types of products A and B and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines M1 and M2. One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2, whereas one unit of type B requires one minute of processing time on M1 and one minute on M2. Machines M1 and M2 are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product should the firm produce a day in order to maximize the profit. Solve the problem graphically.
A library has to accommodate two different types of books on a shelf. The books are 6 cm and 4 cm thick and weigh 1 kg and \[1\frac{1}{2}\] kg each respectively. The shelf is 96 cm long and atmost can support a weight of 21 kg. How should the shelf be filled with the books of two types in order to include the greatest number of books? Make it as an LPP and solve it graphically.
There are two types of fertilizers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds the she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs ₹6/kg and F2 costs ₹5/kg, determine how much of each type of fertilizer should be used so that the nutrient requirements are met at minimum cost. What is the minimum cost?
A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is used to product A and product B. Each unit of product A requires 2, 1 and 1 running feet and each unit of product B requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If product A is sold for Rs. 48 per unit and product B is sold for Rs. 40 per unit, how many units of product A and product B should be produced and sold by the carpenter, in order to obtain the maximum gross income? Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible region in the graph.
Area of the region bounded by y = cos x, x = 0, x = π and X-axis is ______ sq.units.
The feasible region of an LPP is shown in the figure. If z = 3x + 9y, then the minimum value of z occurs at ______.
Maximise and Minimise Z = 3x – 4y subject to x – 2y ≤ 0, – 3x + y ≤ 4, x – y ≤ 6, x, y ≥ 0
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and ____________.
Solve the following Linear Programming problem graphically:
Maximize: Z = 3x + 3.5y
Subject to constraints:
x + 2y ≥ 240,
3x + 1.5y ≥ 270,
1.5x + 2y ≤ 310,
x ≥ 0, y ≥ 0.
Minimize z = x + 2y,
Subject to x + 2y ≥ 50, 2x – y ≤ 0, 2x + y ≤ 100, x ≥ 0, y ≥ 0.
