Advertisements
Advertisements
प्रश्न
A company manufactures two articles A and B. There are two departments through which these articles are processed: (i) assembly and (ii) finishing departments. The maximum capacity of the first department is 60 hours a week and that of other department is 48 hours per week. The product of each unit of article A requires 4 hours in assembly and 2 hours in finishing and that of each unit of B requires 2 hours in assembly and 4 hours in finishing. If the profit is Rs 6 for each unit of A and Rs 8 for each unit of B, find the number of units of A and B to be produced per week in order to have maximum profit.
उत्तर
Let x units and y units of articles A and B are produced respectively.
Number of articles cannot be negative.
Therefore, \[x, y \geq 0\]
The product of each unit of article A requires 4 hours in assembly and that of article B requires 2 hours in assembly and the maximum capacity of the assembly department is 60 hours a week
\[4x + 2y \leq 60\]
The product of each unit of article A requires 2 hours in finishing and that of article B requires 4 hours in assembly and the maximum capacity of the finishing department is 48 hours a week
\[2x + 4y \leq 48\]
If the profit is Rs 6 for each unit of A and Rs 8 for each unit of B. Therefore, profit gained from x units and y units of articles A and B respectively is Rs 6x and Rs 8y respectively.
Total revenue = Z = \[6x + 8y\] which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = \[6x + 8y\]
subject to
\[2x + 4y \leq 48\]
\[4x + 2y \leq 60\]
2x + 4y = 48, 4x + 2y = 60, x = 0 and y = 0
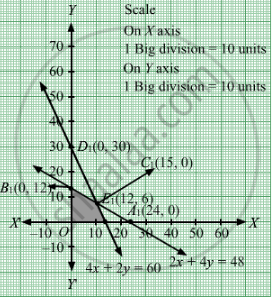
Region represented by 2x + 4y ≤ 48:
The line 2x + 4y = 48 meets the coordinate axes at A1(24, 0) and \[B_1 \left( 0, 12 \right)\] respectively. By joining these points we obtain the line 2x + 4y = 48. Clearly (0,0) satisfies the 2x + 4y = 48. So, the region which contains the origin represents the solution set of the inequation 2x + 4y ≤ 48.
Region represented by 4x + 2y ≤ 60:
The line 4x + 2y = 60 meets the coordinate axes at C1(15, 0) and \[D_1 \left( 0, 30 \right)\] respectively. By joining these points we obtain the line 4x + 2y = 60. Clearly (0,0) satisfies the inequation 4x + 2y ≤ 60. So,the region which contains the origin represents the solution set of the inequation 4x + 2y ≤ 60.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2x + 4y ≤ 48, 4x + 2y ≤ 60, x ≥ 0 and y ≥ 0 are as follows.
 T
T
he corner points are O(0, 0), B1(0, 12), E1(12, 6) and C1(15,0).
The values of Z at these corner points are as follows
| Corner point | Z= 6x + 8y |
| O | 0 |
| B1 | 96 |
| E1 | 120 |
| C1 | 90 |
The maximum value of Z is 120 which is attained at E1(12, 6).
Thus, the maximum profit is Rs 120 obtained when 12 units of article A and 6 units of article B were manufactured.
APPEARS IN
संबंधित प्रश्न
Minimize `z=4x+5y ` subject to `2x+y>=7, 2x+3y<=15, x<=3,x>=0, y>=0` solve using graphical method.
Solve the following L.P.P graphically:
Maximize: Z = 10x + 25y
Subject to: x ≤ 3, y ≤ 3, x + y ≤ 5, x ≥ 0, y ≥ 0
Minimize :Z=6x+4y
Subject to : 3x+2y ≥12
x+y ≥5
0 ≤x ≤4
0 ≤ y ≤ 4
There are two types of fertilisers 'A' and 'B'. 'A' consists of 12% nitrogen and 5% phosphoric acid whereas 'B' consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If 'A' costs Rs 10 per kg and 'B' cost Rs 8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost
Maximise z = 8x + 9y subject to the constraints given below :
2x + 3y ≤ 6
3x − 2y ≤6
y ≤ 1
x, y ≥ 0
Minimize Z = 30x + 20y
Subject to
\[x + y \leq 8\]
\[ x + 4y \geq 12\]
\[5x + 8y = 20\]
\[ x, y \geq 0\]
Maximize Z = −x1 + 2x2
Subject to
\[- x_1 + 3 x_2 \leq 10\]
\[ x_1 + x_2 \leq 6\]
\[ x_1 - x_2 \leq 2\]
\[ x_1 , x_2 \geq 0\]
Find the maximum and minimum value of 2x + y subject to the constraints:
x + 3y ≥ 6, x − 3y ≤ 3, 3x + 4y ≤ 24, − 3x + 2y ≤ 6, 5x + y ≥ 5, x, y ≥ 0.
Solved the following linear programming problem graphically:
Maximize Z = 60x + 15y
Subject to constraints
\[x + y \leq 50\]
\[3x + y \leq 90\]
\[ x, y \geq 0\]
A diet of two foods F1 and F2 contains nutrients thiamine, phosphorous and iron. The amount of each nutrient in each of the food (in milligrams per 25 gms) is given in the following table:
Nutrients |
Food |
F1 | F2 |
| Thiamine | 0.25 | 0.10 |
|
| Phosphorous | 0.75 | 1.50 | |
| Iron | 1.60 | 0.80 | |
The minimum requirement of the nutrients in the diet are 1.00 mg of thiamine, 7.50 mg of phosphorous and 10.00 mg of iron. The cost of F1 is 20 paise per 25 gms while the cost of F2 is 15 paise per 25 gms. Find the minimum cost of diet.
A publisher sells a hard cover edition of a text book for Rs 72.00 and paperback edition of the same ext for Rs 40.00. Costs to the publisher are Rs 56.00 and Rs 28.00 per book respectively in addition to weekly costs of Rs 9600.00. Both types require 5 minutes of printing time, although hardcover requires 10 minutes binding time and the paperback requires only 2 minutes. Both the printing and binding operations have 4,800 minutes available each week. How many of each type of book should be produced in order to maximize profit?
A manufacturer produces two types of steel trunks. He has two machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively. How many trunks of each type must he make each day to make maximum profit?
An oil company has two depots, A and B, with capacities of 7000 litres and 4000 litres respectively. The company is to supply oil to three petrol pumps, D, E, F whose requirements are 4500, 3000 and 3500 litres respectively. The distance (in km) between the depots and petrol pumps is given in the following table:
Figure
Assuming that the transportation cost per km is Rs 1.00 per litre, how should the delivery be scheduled in order that the transportation cost is minimum?
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time. If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the number of tennis rackets and cricket bats that the factory must manufacture to earn the maximum profit. Make it as an LPP and solve it graphically.
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000. Make an LPP and solve it graphically.
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Types of Toys | Machines | ||
| I | II | III | |
| A | 12 | 18 | 6 |
| B | 6 | 0 | 9 |
An aeroplane can carry a maximum of 200 passengers. A profit of ₹1000 is made on each executive class ticket and a profit of ₹600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However, atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit of the airline. What is the maximum profit?
Maximize: z = 3x + 5y Subject to
x +4y ≤ 24 3x + y ≤ 21
x + y ≤ 9 x ≥ 0 , y ≥0
From the details given below, calculate the five-year moving averages of the number of students who have studied in a school. Also, plot these and original data on the same graph paper.
| Year | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| Number of Students | 332 | 317 | 357 | 392 | 402 | 405 | 410 | 427 | 405 | 438 |
A company manufactures two types of cardigans: type A and type B. It costs ₹ 360 to make a type A cardigan and ₹ 120 to make a type B cardigan. The company can make at most 300 cardigans and spend at most ₹ 72000 a day. The number of cardigans of type B cannot exceed the number of cardigans of type A by more than 200. The company makes a profit of ₹ 100 for each cardigan of type A and ₹ 50 for every cardigan of type B.
Formulate this problem as a linear programming problem to maximize the profit to the company. Solve it graphically and find the maximum profit.
Sketch the graph of inequation x ≥ 5y in xoy co-ordinate system
Draw the graph of inequalities x ≤ 6, y −2 ≤ 0, x ≥ 0, y ≥ 0 and indicate the feasible region
The minimum value of z = 10x + 25y subject to 0 ≤ x ≤ 3, 0 ≤ y ≤ 3, x + y ≥ 5 is ______.
For the LPP, maximize z = x + 4y subject to the constraints x + 2y ≤ 2, x + 2y ≥ 8, x, y ≥ 0 ______.
In linear programming feasible region (or solution region) for the problem is ____________.
In Corner point method for solving a linear programming problem the first step is to ____________.
The corner points of the bounded feasible region of a LPP are A(0,50), B(20, 40), C(50, 100) and D(0, 200) and the objective function is Z = x + 2y. Then the maximum value is ____________.
A manufacturer wishes to produce two commodities A and B. The number of units of material, labour and equipment needed to produce one unit of each commodity is shown in the table given below. Also shown is the available number of units of each item, material, labour, and equipment.
| Items | Commodity A | Commodity B | Available no. of Units |
| Material | 1 | 2 | 8 |
| Labour | 3 | 2 | 12 |
| Equipment | 1 | 1 | 10 |
Find the maximum profit if each unit of commodity A earns a profit of ₹ 2 and each unit of B earns a profit of ₹ 3.
Minimise z = – 3x + 4y subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0 What will be the minimum value of z ?
Any point in the feasible region that gives the optional value (maximum or minimum) of the objective function is called:-
The maximum value of 2x + y subject to 3x + 5y ≤ 26 and 5x + 3y ≤ 30, x ≥ 0, y ≥ 0 is ______.
Solve the following Linear Programming Problem graphically:
Maximize: P = 70x + 40y
Subject to: 3x + 2y ≤ 9,
3x + y ≤ 9,
x ≥ 0,y ≥ 0.
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
Which of the following is not a constraint to the given Linear Programming Problem?
Solve the following Linear Programming Problem graphically:
Minimize: z = x + 2y,
Subject to the constraints: x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200, x, y ≥ 0.
Find feasible solution for the following system of linear inequation graphically.
3x + 4y ≥ 12, 4x + 7y ≤ 28, x ≥ 0, y ≥ 0
A linear programming problem is given by Z = px + qy where p, q > 0 subject to the constraints: x + y ≤ 60, 5x + y ≤ 100, x ≥ 0 and y ≥ 0
- Solve graphically to find the corner points of the feasible region.
- If Z = px + qy is maximum at (0, 60) and (10, 50), find the relation of p and q. Also mention the number of optimal solution(s) in this case.
