Advertisements
Advertisements
प्रश्न
A gardener has supply of fertilizer of type I which consists of 10% nitrogen and 6% phosphoric acid and type II fertilizer which consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, he finds that he needs at least 14 kg of nitrogen and 14 kg of phosphoric acid for his crop. If the type I fertilizer costs 60 paise per kg and type II fertilizer costs 40 paise per kg, determine how many kilograms of each fertilizer should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost?
उत्तर
Let x kg of type I fertilizer and y kg of type II fertilizer are supplied.
Quantity of fertilizer cannot be negative.
Therefore, \[x, y \geq 0\]
A gardener has supply of fertilizer of type I which consists of 10% nitrogen and type II fertilizer consists of 5% nitrogen and he needs at least 14 kg of nitrogen for his crop.\[\frac{10x}{100} + \frac{5x}{100} \geq 14 \Rightarrow 10x + 5x \geq 1400\]
A gardener has supply of fertilizer of type I which consists 6% phosphoric acid and type II fertilizer consists of 10% phosphoric acid.
And he needs 14 kg of phosphoric acid for his crop.
Therefore, according to the question, constraints are
\[10x + 5y \geq 1400\]
\[6x + 10y \geq 1400\]
Total cost = Z =\[0 . 60x + 0 . 40y\] which is to be minimised.
Min Z = \[0 . 60x + 0 . 40y\]subject to
\[10x + 5y \geq 1400\]
\[x, y \geq 0\]
6x + 10y = 1400, 10x + 5y = 1400, x = 0 and y = 0
Region represented by 6x + 10y ≥ 1400:
The line 6x + 10y = 1400 meets the coordinate axes at
Region represented by 10x + 5y ≥ 1400:
The line 10x + 5y = 1400 meets the coordinate axes at C(140, 0) and \[D\left( 0, 280 \right)\] respectively. By joining these points we obtain the line 10x + 5y = 1400. Clearly (0,0) does not satisfies the inequation 10x + 5y ≥ 1400. So,the region which does not contain the origin represents the solution set of the inequation 10x + 5y ≥ 1400.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 6x + 10y ≥1400, 10x + 5y ≥ 1400, x ≥ 0 and y ≥ 0 are as follows.
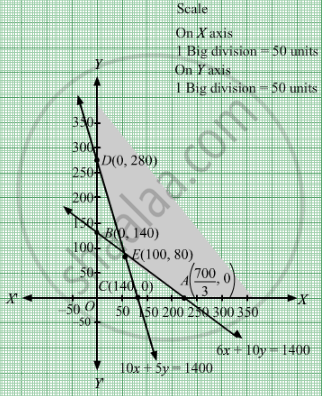
| Corner point | Z= 0.60x + 0.40y |
| D | 112 |
| E | 92 |
| A | 140 |
The minimum value of Z is Rs 92 which is attained at E(100, 80).
Thus, the minimum cost is Rs 92 obtained when 100 kg of type I fertilizer and 80 kg of type II fertilizer were supplied.
APPEARS IN
संबंधित प्रश्न
There are two types of fertilisers 'A' and 'B'. 'A' consists of 12% nitrogen and 5% phosphoric acid whereas 'B' consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If 'A' costs Rs 10 per kg and 'B' cost Rs 8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost
Maximize Z = 50x + 30y
Subject to
\[2x + y \leq 18\]
\[3x + 2y \leq 34\]
\[ x, y \geq 0\]
Maximize Z = 3x1 + 4x2, if possible,
Subject to the constraints
\[x_1 - x_2 \leq - 1\]
\[ - x_1 + x_2 \leq 0\]
\[ x_1 , x_2 \geq 0\]
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
One kg of food X costs ₹16 and one kg of food Y costs ₹20. Find the least cost of the mixture which will produce the required diet?
A fruit grower can use two types of fertilizer in his garden, brand P and Q. The amounts (in kg) of nirogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicates that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.
| kg per bag | ||
| Brand P | Brand P | |
| Nitrogen | 3 | 3.5 |
| Phosphoric acid | 1 | 2 |
| Potash | 3 | 1.5 |
| Chlorine | 1.5 | 2 |
If the grower wants to minimize the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?
A manufacturer has three machines installed in his factory. machines I and II are capable of being operated for at most 12 hours whereas Machine III must operate at least for 5 hours a day. He produces only two items, each requiring the use of three machines. The number of hours required for producing one unit each of the items on the three machines is given in the following table:
| Item | Number of hours required by the machine | ||
A B |
I | II | III |
| 1 2 |
2 1 |
1 5/4 |
|
He makes a profit of Rs 6.00 on item A and Rs 4.00 on item B. Assuming that he can sell all that he produces, how many of each item should he produces so as to maximize his profit? Determine his maximum profit. Formulate this LPP mathematically and then solve it.
A factory manufactures two types of screws, A and B, each type requiring the use of two machines - an automatic and a hand-operated. It takes 4 minute on the automatic and 6 minutes on the hand-operated machines to manufacture a package of screws 'A', while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machine to manufacture a package of screws 'B'. Each machine is available for at most 4 hours on any day. The manufacturer can sell a package of screws 'A' at a profit of 70 P and screws 'B' at a profit of Rs 1. Assuming that he can sell all the screws he can manufacture, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.
A manufacturer makes two products A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 of product A and 16 of product B. A working week consists of 40 hours of production and weekly turnover must not be less than Rs 10000. If the profit on each of product A is Rs 20 and on product B is Rs 30, then how many of each should be produced so that the profit is maximum. Also, find the maximum profit.
A producer has 30 and 17 units of labour and capital respectively which he can use to produce two type of goods x and y. To produce one unit of x, 2 units of labour and 3 units of capital are required. Similarly, 3 units of labour and 1 unit of capital is required to produce one unit of y. If x and y are priced at Rs 100 and Rs 120 per unit respectively, how should be producer use his resources to maximize the total revenue? Solve the problem graphically.
A company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs 50 each on type A and Rs 60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
A company manufactures two articles A and B. There are two departments through which these articles are processed: (i) assembly and (ii) finishing departments. The maximum capacity of the first department is 60 hours a week and that of other department is 48 hours per week. The product of each unit of article A requires 4 hours in assembly and 2 hours in finishing and that of each unit of B requires 2 hours in assembly and 4 hours in finishing. If the profit is Rs 6 for each unit of A and Rs 8 for each unit of B, find the number of units of A and B to be produced per week in order to have maximum profit.
A company sells two different products, A and B. The two products are produced in a common production process, which has a total capacity of 500 man-hours. It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B. The market has been surveyed and company officials feel that the maximum number of unit of A that can be sold is 70 and that for B is 125. If the profit is Rs 20 per unit for the product A and Rs 15 per unit for the product B, how many units of each product should be sold to maximize profit?
A box manufacturer makes large and small boxes from a large piece of cardboard. The large boxes require 4 sq. metre per box while the small boxes require 3 sq. metre per box. The manufacturer is required to make at least three large boxes and at least twice as many small boxes as large boxes. If 60 sq. metre of cardboard is in stock, and if the profits on the large and small boxes are Rs 3 and Rs 2 per box, how many of each should be made in order to maximize the total profit?
An oil company has two depots, A and B, with capacities of 7000 litres and 4000 litres respectively. The company is to supply oil to three petrol pumps, D, E, F whose requirements are 4500, 3000 and 3500 litres respectively. The distance (in km) between the depots and petrol pumps is given in the following table:
Figure
Assuming that the transportation cost per km is Rs 1.00 per litre, how should the delivery be scheduled in order that the transportation cost is minimum?
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time. If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the number of tennis rackets and cricket bats that the factory must manufacture to earn the maximum profit. Make it as an LPP and solve it graphically.
An aeroplane can carry a maximum of 200 passengers. A profit of ₹1000 is made on each executive class ticket and a profit of ₹600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However, atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit of the airline. What is the maximum profit?
The region represented by the inequation system x, y ≥ 0, y ≤ 6, x + y ≤ 3 is
A farmer has a supply of chemical fertilizer of type A which contains 10% nitrogen and 6% phosphoric acid and of type B which contains 5% nitrogen and 10% phosphoric acid. After the soil test, it is found that at least 7 kg of nitrogen and the same quantity of phosphoric acid is required for a good crop. The fertilizer of type A costs ₹ 5.00 per kg and the type B costs ₹ 8.00 per kg. Using Linear programming, find how many kilograms of each type of fertilizer should be bought to meet the requirement and for the cost to be minimum. Find the feasible region in the graph.
A company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is ₹ 40 on each unit of the product of type A and ₹ 50 on each unit of type B. How many units of each type should the company manufacture so as to earn a maximum profit? Use linear programming to find the solution.
A company manufactures two types of cardigans: type A and type B. It costs ₹ 360 to make a type A cardigan and ₹ 120 to make a type B cardigan. The company can make at most 300 cardigans and spend at most ₹ 72000 a day. The number of cardigans of type B cannot exceed the number of cardigans of type A by more than 200. The company makes a profit of ₹ 100 for each cardigan of type A and ₹ 50 for every cardigan of type B.
Formulate this problem as a linear programming problem to maximize the profit to the company. Solve it graphically and find the maximum profit.
The graph of the inequality 3X − 4Y ≤ 12, X ≤ 1, X ≥ 0, Y ≥ 0 lies in fully in
Sketch the graph of inequation x ≥ 5y in xoy co-ordinate system
Maximum value of 4x + 13y subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is ______.
The minimum value of z = 7x + 9y subject to 3x + y ≤ 6, 5x + 8y ≤ 40, x ≥ 0, y ≥ 2 is ______.
Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is ______.
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and ____________.
Minimise z = – 3x + 4y subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0 What will be the minimum value of z ?
The maximum value of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
The objective function Z = ax + by of an LPP has maximum vaiue 42 at (4, 6) and minimum value 19 at (3, 2). Which of the following is true?
Solve the following linear programming problem graphically:
Maximize: Z = x + 2y
Subject to constraints:
x + 2y ≥ 100,
2x – y ≤ 0
2x + y ≤ 200,
x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problem graphically:
Maximize: P = 70x + 40y
Subject to: 3x + 2y ≤ 9,
3x + y ≤ 9,
x ≥ 0,y ≥ 0.
Solve the following Linear Programming Problem graphically:
Minimize: Z = 60x + 80y
Subject to constraints:
3x + 4y ≥ 8
5x + 2y ≥ 11
x, y ≥ 0
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
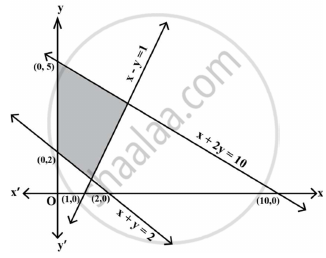
Which of the following is not a constraint to the given Linear Programming Problem?
Solve the following Linear Programming Problem graphically:
Minimize: z = x + 2y,
Subject to the constraints: x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200, x, y ≥ 0.
Find feasible solution for the following system of linear inequation graphically.
3x + 4y ≥ 12, 4x + 7y ≤ 28, x ≥ 0, y ≥ 0
