Advertisements
Advertisements
प्रश्न
Minimize Z = 2x + 4y
Subject to
\[x + y \geq 8\]
\[x + 4y \geq 12\]
\[x \geq 3, y \geq 2\]
उत्तर
First, we will convert the given inequations into equations, we obtain the following equations:
x + y = 8, x + 4y = 12, x = 3, y = 2
Region represented by x + y ≥ 8:
The line x + y = 8 meets the coordinate axes at A(8, 0) and B(0, 8) respectively. By joining these points we obtain the line x + y = 8.
Clearly (0,0) does not satisfies the inequation x + y ≥ 8. So,the region in xy plane which does not contain the origin represents the solution set of the inequation x + y ≥ 8.
Region represented by x + 4y ≥ 12:
The line x + 4y = 12 meets the coordinate axes at C(12, 0) and D(0, 3) respectively. By joining these points we obtain the line x + 4y = 12.
Clearly (0,0) satisfies the inequation x + 4y ≥ 12. So,the region in xy plane which contain the origin represents the solution set of the inequation x + 4y ≥ 12.
The line x = 3 is the line that passes through the point (3, 0) and is parallel to Y axis.x ≥ 3 is the region to the right of the line x = 3.
The line y = 2 is the line that passes through the point (0, 12) and is parallel to X axis.y ≥ 2 is the region above the line y = 2.
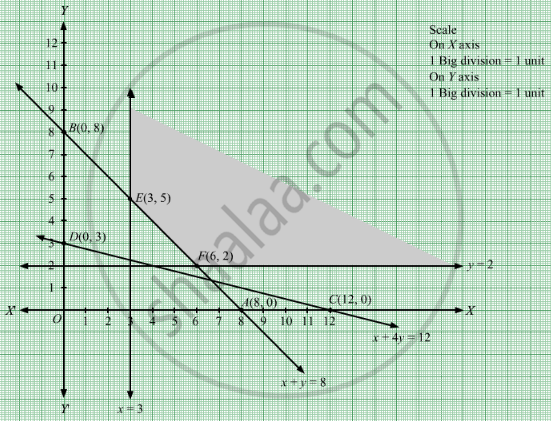
The corner points of the feasible region are E(3, 5) and F(6, 2).
The values of Z at these corner points are as follows.
| Corner point | Z = 2x + 4y |
| E(3, 5) | 2 × 3 + 4 × 5 = 26 |
| F(6, 2) | 2 × 6 + 4 × 2 = 20 |
Therefore, the minimum value of Z is 20 at the point F(6, 2). Hence, x = 6 and y =2 is the optimal solution of the given LPP.
Thus, the optimal value of Z is 20.
APPEARS IN
संबंधित प्रश्न
Solve the following LPP by using graphical method.
Maximize : Z = 6x + 4y
Subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
Also find maximum value of Z.
Solve the following L.P.P graphically:
Maximize: Z = 10x + 25y
Subject to: x ≤ 3, y ≤ 3, x + y ≤ 5, x ≥ 0, y ≥ 0
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30, respectively. The company makes a profit of Rs 80 on each piece of type A and Rs 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week?
Maximize Z = 15x + 10y
Subject to
\[3x + 2y \leq 80\]
\[2x + 3y \leq 70\]
\[ x, y \geq 0\]
Maximize Z = 3x + 4y
Subject to
\[2x + 2y \leq 80\]
\[2x + 4y \leq 120\]
Maximize Z = 7x + 10y
Subject to
\[x + y \leq 30000\]
\[ y \leq 12000\]
\[ x \geq 6000\]
\[ x \geq y\]
\[ x, y \geq 0\]
Maximize Z = 2x + 3y
Subject to
\[x + y \geq 1\]
\[10x + y \geq 5\]
\[x + 10y \geq 1\]
\[ x, y \geq 0\]
Find the maximum and minimum value of 2x + y subject to the constraints:
x + 3y ≥ 6, x − 3y ≤ 3, 3x + 4y ≤ 24, − 3x + 2y ≤ 6, 5x + y ≥ 5, x, y ≥ 0.
Solved the following linear programming problem graphically:
Maximize Z = 60x + 15y
Subject to constraints
\[x + y \leq 50\]
\[3x + y \leq 90\]
\[ x, y \geq 0\]
A dietician mixes together two kinds of food in such a way that the mixture contains at least 6 units of vitamin A, 7 units of vitamin B, 11 units of vitamin C and 9 units of vitamin D. The vitamin contents of 1 kg of food X and 1 kg of food Y are given below:
| Vitamin A |
Vitamin B |
Vitamin |
Vitamin D |
|
| Food X Food Y |
1 2 |
1 1 |
1 3 |
2 1 |
One kg food X costs Rs 5, whereas one kg of food Y costs Rs 8. Find the least cost of the mixture which will produce the desired diet.
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1and F2 are available. Food F1 costs Rs 4 per unit and F2 costs Rs 6 per unit one unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem and find graphically the minimum cost for diet that consists of mixture of these foods and also meets the mineral nutritional requirements
One kind of cake requires 300 gm of flour and 15 gm of fat, another kind of cake requires 150 gm of flour and 30 gm of fat. Find the maximum number of cakes which can be made from 7.5 kg of flour and 600 gm of fat, assuming that there is no shortage of the other ingradients used in making the cake. Make it as an LPP and solve it graphically.
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
One kg of food X costs ₹16 and one kg of food Y costs ₹20. Find the least cost of the mixture which will produce the required diet?
A small manufacturer has employed 5 skilled men and 10 semi-skilled men and makes an article in two qualities deluxe model and an ordinary model. The making of a deluxe model requires 2 hrs. work by a skilled man and 2 hrs. work by a semi-skilled man. The ordinary model requires 1 hr by a skilled man and 3 hrs. by a semi-skilled man. By union rules no man may work more than 8 hrs per day. The manufacturers clear profit on deluxe model is Rs 15 and on an ordinary model is Rs 10. How many of each type should be made in order to maximize his total daily profit.
A furniture manufacturing company plans to make two products : chairs and tables. From its available resources which consists of 400 square feet to teak wood and 450 man hours. It is known that to make a chair requires 5 square feet of wood and 10 man-hours and yields a profit of Rs 45, while each table uses 20 square feet of wood and 25 man-hours and yields a profit of Rs 80. How many items of each product should be produced by the company so that the profit is maximum?
A publisher sells a hard cover edition of a text book for Rs 72.00 and paperback edition of the same ext for Rs 40.00. Costs to the publisher are Rs 56.00 and Rs 28.00 per book respectively in addition to weekly costs of Rs 9600.00. Both types require 5 minutes of printing time, although hardcover requires 10 minutes binding time and the paperback requires only 2 minutes. Both the printing and binding operations have 4,800 minutes available each week. How many of each type of book should be produced in order to maximize profit?
A company manufactures two types of novelty Souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours available for assembling. The profit is 50 paise each for type A and 60 paise each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
A firm makes items A and B and the total number of items it can make in a day is 24. It takes one hour to make an item of A and half an hour to make an item of B. The maximum time available per day is 16 hours. The profit on an item of A is Rs 300 and on one item of B is Rs 160. How many items of each type should be produced to maximize the profit? Solve the problem graphically.
A box manufacturer makes large and small boxes from a large piece of cardboard. The large boxes require 4 sq. metre per box while the small boxes require 3 sq. metre per box. The manufacturer is required to make at least three large boxes and at least twice as many small boxes as large boxes. If 60 sq. metre of cardboard is in stock, and if the profits on the large and small boxes are Rs 3 and Rs 2 per box, how many of each should be made in order to maximize the total profit?
If a young man drives his vehicle at 25 km/hr, he has to spend ₹2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to ₹5 per km. He has ₹100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
A small firm manufactures gold rings and chains. The total number of rings and chains manufactured per day is at most 24. It takes 1 hour to make a ring and 30 minutes to make a chain. The maximum number of hours available per day is 16. If the profit on a ring is Rs 300 and that on a chain is Rs 190, find the number of rings and chains that should be manufactured per day, so as to earn the maximum profit. Make it as an LPP and solve it graphically.
Tow godowns, A and B, have grain storage capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F, whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
| Transportation cost per quintal(in Rs.) | ||
| From-> | A | B |
| To | ||
| D | 6.00 | 4.00 |
| E | 3.00 | 2.00 |
| F | 2.50 | 3.00 |
How should the supplies be transported in order that the transportation cost is minimum?
The value of objective function is maximum under linear constraints ______.
Maximize: z = 3x + 5y Subject to
x +4y ≤ 24 3x + y ≤ 21
x + y ≤ 9 x ≥ 0 , y ≥0
Find the graphical solution for the system of linear inequation 2x + y ≤ 2, x − y ≤ 1
For the function z = 19x + 9y to be maximum under the constraints 2x + 3y ≤ 134, x + 5y ≤ 200, x ≥ 0, y ≥ 0; the values of x and y are ______.
The maximum value of z = 3x + 10y subjected to the conditions 5x + 2y ≤ 10, 3x + 5y ≤ 15, x, y ≥ 0 is ______.
Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is ______.
A feasible region in the set of points which satisfy ____________.
A set of values of decision variables which satisfies the linear constraints and nn-negativity conditions of an L.P.P. is called its ____________.
In linear programming feasible region (or solution region) for the problem is ____________.
In Corner point method for solving a linear programming problem the first step is to ____________.
The shaded part of given figure indicates in feasible region, then the constraints are:

Solve the following linear programming problem graphically:
Minimize: Z = 5x + 10y
Subject to constraints:
x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problem graphically:
Minimize: Z = 60x + 80y
Subject to constraints:
3x + 4y ≥ 8
5x + 2y ≥ 11
x, y ≥ 0
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
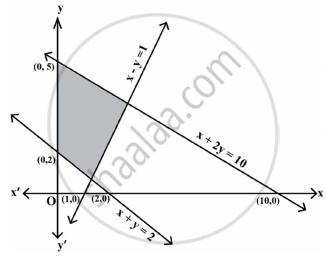
Which of the following is not a constraint to the given Linear Programming Problem?
Solve the following Linear Programming Problem graphically:
Maximize: z = – x + 2y,
Subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
