Advertisements
Advertisements
प्रश्न
Evaluate: `int_1^4 {|x -1|+|x - 2|+|x - 4|}dx`
उत्तर १
I = `int_1^4 (|x -1|+|x - 2|+|x - 4|)dx`
Let f (x) = |x - 1| + |x - 2| + |x - 4|
We have three critical points x = 1, 2, 4
(i) when x <1
(ii) when 1≤ x < 2
(iii) when 2 ≤ x < 4
(iv) when x ≥ 4

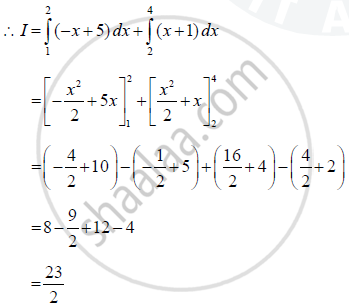
उत्तर २

संबंधित प्रश्न
`int_(-pi/2)^(pi/2) (x^3 + x cos x + tan^5 x + 1) dx ` is ______.
Evaluate the definite integrals `int_0^pi (x tan x)/(sec x + tan x)dx`
Evaluate : `int _0^(pi/2) "sin"^ 2 "x" "dx"`
Evaluate : `int "e"^(3"x")/("e"^(3"x") + 1)` dx
Evaluate the following integrals : `int_2^5 sqrt(x)/(sqrt(x) + sqrt(7 - x))*dx`
`int_"a"^"b" "f"(x) "d"x` = ______
`int_0^1 ((x^2 - 2)/(x^2 + 1))`dx = ?
The c.d.f, F(x) associated with p.d.f. f(x) = 3(1- 2x2). If 0 < x < 1 is k`(x - (2x^3)/"k")`, then value of k is ______.
`int_0^1 (1 - x/(1!) + x^2/(2!) - x^3/(3!) + ... "upto" ∞)` e2x dx = ?
`int_"a"^"b" sqrtx/(sqrtx + sqrt("a" + "b" - x)) "dx"` = ______.
`int_(pi/18)^((4pi)/9) (2 sqrt(sin x))/(sqrt (sin x) + sqrt(cos x))` dx = ?
Show that `int_0^(pi/2) (sin^2x)/(sinx + cosx) = 1/sqrt(2) log (sqrt(2) + 1)`
Evaluate the following:
`int_(-pi/4)^(pi/4) log|sinx + cosx|"d"x`
The value of `int_0^1 tan^-1 ((2x - 1)/(1 + x - x^2)) dx` is
Evaluate: `int_0^(π/2) 1/(1 + (tanx)^(2/3)) dx`
Evaluate: `int_0^(2π) (1)/(1 + e^(sin x)`dx
Evaluate: `int_(-1)^3 |x^3 - x|dx`
Evaluate: `int_2^5 sqrt(x)/(sqrt(x) + sqrt(7) - x)dx`
`int_0^π(xsinx)/(1 + cos^2x)dx` equals ______.
What is `int_0^(π/2)` sin 2x ℓ n (cot x) dx equal to ?
`int_(π/3)^(π/2) x sin(π[x] - x)dx` is equal to ______.
If `int_0^(2π) cos^2 x dx = k int_0^(π/2) cos^2 x dx`, then the value of k is ______.
Evaluate: `int_(-π//4)^(π//4) (cos 2x)/(1 + cos 2x)dx`.
Evaluate: `int_0^π x/(1 + sinx)dx`.
Evaluate the following definite integral:
`int_4^9 1/sqrt"x" "dx"`
Evaluate the following integral:
`int_0^1 x(1 - 5)^5`dx
If `int_0^1(3x^2 + 2x+a)dx = 0,` then a = ______
Evaluate:
`int_0^6 |x + 3|dx`
Evaluate the following integral:
`int_0^1x(1 - x)^5dx`
Evaluate the following definite integral:
`int_-2^3(1)/(x + 5) dx`
