Advertisements
Advertisements
प्रश्न
Evaluate: `int_1^4 {|x -1|+|x - 2|+|x - 4|}dx`
उत्तर १
I = `int_1^4 (|x -1|+|x - 2|+|x - 4|)dx`
Let f (x) = |x - 1| + |x - 2| + |x - 4|
We have three critical points x = 1, 2, 4
(i) when x <1
(ii) when 1≤ x < 2
(iii) when 2 ≤ x < 4
(iv) when x ≥ 4

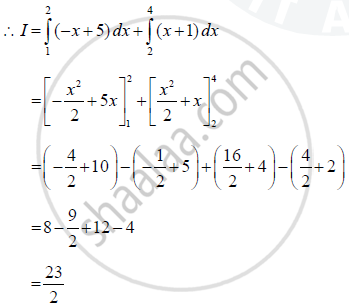
उत्तर २

संबंधित प्रश्न
Prove that: `int_0^(2a)f(x)dx=int_0^af(x)dx+int_0^af(2a-x)dx`
Evaluate : `intsec^nxtanxdx`
By using the properties of the definite integral, evaluate the integral:
`int_0^4 |x - 1| dx`
`int_(-pi/2)^(pi/2) (x^3 + x cos x + tan^5 x + 1) dx ` is ______.
Evaluate : \[\int(3x - 2) \sqrt{x^2 + x + 1}dx\] .
Find `dy/dx, if y = cos^-1 ( sin 5x)`
Evaluate: `int_0^pi ("x"sin "x")/(1+ 3cos^2 "x") d"x"`.
Evaluate `int_0^1 x(1 - x)^5 "d"x`
`int_0^(pi/4) (sec^2 x)/((1 + tan x)(2 + tan x))`dx = ?
The value of `int_-3^3 ("a"x^5 + "b"x^3 + "c"x + "k")"dx"`, where a, b, c, k are constants, depends only on ______.
`int_0^(pi/2) sqrt(cos theta) * sin^2 theta "d" theta` = ______.
`int_0^{pi/4} (sin2x)/(sin^4x + cos^4x)dx` = ____________
`int_0^(pi/2) 1/(1 + cosx) "d"x` = ______.
Evaluate `int_0^(pi/2) (tan^7x)/(cot^7x + tan^7x) "d"x`
Show that `int_0^(pi/2) (sin^2x)/(sinx + cosx) = 1/sqrt(2) log (sqrt(2) + 1)`
If `int (log "x")^2/"x" "dx" = (log "x")^"k"/"k" + "c"`, then the value of k is:
`int_(-5)^5 x^7/(x^4 + 10) dx` = ______.
Evaluate: `int_0^(2π) (1)/(1 + e^(sin x)`dx
`int_0^1 1/(2x + 5) dx` = ______.
`int_a^b f(x)dx = int_a^b f(x - a - b)dx`.
The value of the integral `int_(-1)^1log_e(sqrt(1 - x) + sqrt(1 + x))dx` is equal to ______.
`int_0^(pi/4) (sec^2x)/((1 + tanx)(2 + tanx))dx` equals ______.
Evaluate `int_-1^1 |x^4 - x|dx`.
Evaluate the following integral:
`int_-9^9 x^3/(4-x^2)dx`
Evaluate the following integral:
`int_0^1 x(1-x)^5 dx`
Solve.
`int_0^1e^(x^2)x^3dx`
Solve the following.
`int_0^1e^(x^2)x^3dx`
Evaluate:
`int_0^6 |x + 3|dx`
Evaluate the following integral:
`int_0^1x(1-x)^5dx`
Solve the following.
`int_0^1e^(x^2)x^3dx`
