Advertisements
Advertisements
प्रश्न
निचे दी गई आकृति यदि ∠a ≅ ∠b तो सिद्ध कीजिए कि रेखा l || रेखा m

उत्तर
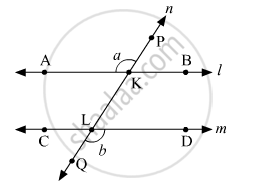
रेखा l पर बिंदु A और B, रेखा m पर बिंदु C और D तथा रेखा n पर बिंदु P और Q अंकित करें।
मान लीजिए कि रेखा n, रेखा l को K पर और रेखा m को L पर प्रतिच्छेदित करती है।
तथा PQ एक सीधी रेखा है और किरण KA उस पर खड़ी है
m∠AKP + m∠AKL = 180∘ ....(रैखिय युगल कोण)
⇒m∠a + m∠AKL = 180∘
⇒m∠a = 180∘ − m∠AKL ....(1)
तथा PQ एक सीधी रेखा है और किरण LD उस पर खड़ी है
m∠DLQ + m∠DLK = 180∘ .....(रैखिय युगल कोण)
⇒m∠b + m∠DLK = 180∘
⇒m∠b = 180∘ − m∠DLK ....(2)
यदि ∠a ≅ ∠b, तो m∠a = m∠b
[(i) और (ii) से]
180∘ − m∠AKL = 180∘ − m∠DLK
⇒m∠AKL = m∠DLK
⇒∠AKL ≅ ∠DLK
यह ज्ञात है कि, यदि दो रेखाओं के तिर्यक छेद से बना एकांतर आंतरिक कोणों का एक युग्म सर्वांगसम हो, तो दोनों रेखाएँ समानांतर होती हैं।
∴ AB || CD या रेखा l || रेखा m.
APPEARS IN
संबंधित प्रश्न
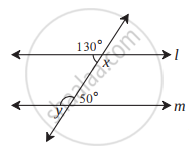
आकृति में, y = 108° तथा x = 71° तो रेखा m तथा रेखा n समांतर होगी, कारण लिखिए।
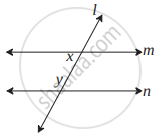
आकृति में यदि ∠a ≅ ∠b और ∠x ≅ ∠y तो सिद्ध कीजिए कि रेखा l || रेखा n

दो रेखाओं को किसी तिर्यक रेखा द्वारा प्रतिच्छेदित करने पर ______ कोण निर्मित होते हैं ।
ΔABC में ∠A = 76°, ∠B = 48°, तो ∠C का माप ______ है ।
दो समांतर रेखाओं को किसी तिर्यक रेखा द्वारा प्रतिच्छेदित करने पर बनने वाले एकांतर कोणों की जोड़ी में से यदि एक कोण का माप 75° हो तो दूसरे कोण का माप ______ होता है।
निचे दी गई आकृति में दिए गए कोणों के मापों के आधार पर ∠x तथा ∠y के माप ज्ञात करे। सिद्ध कीजिए कि रेखा l || रेखा m
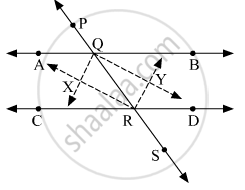
निचे दी गई आकृति के आधार पर रेखा AB || रेखा CD तथा रेखा PS उसकी तिर्यक रेखा है। किरण QX, किरण QY, किरण RX तथा किरण RY यह कोणों की समद्विभाजक है। तो सिद्ध कीजिए कि `square` QXRY एक आयत है।