Advertisements
Advertisements
प्रश्न
नीचे दी हुई सारणी कुछ सामान्य पदार्थों के उन भागों को प्रदर्शित करती है, जो पुनः प्रयुक्त किये जाते है –
| पदार्थ | पुनः प्रयुक्त |
| कागज | `5/11` |
| एल्युमिनियम के डिब्बे | `5/8` |
| काँच | `2/5` |
| अन्य | `3/4` |
- क्या कागज को पुनः प्रयुक्त व्यक्त करने वाली परिमेय संख्या `1/2` से अधिक है या `1/2` से छोटी है?
- किन पदार्थों की पुनः प्रयुक्त मात्रा `1/2` से कम है?
- एल्युमिनियम के डिब्बों की पुनः प्रयुक्त मात्रा एल्युमिनियम के डिब्बों की मात्रा के आधे से अधिक है या कम है?
- बड़े से छोटे क्रम में पुनः प्रयुक्त मात्राओं को व्यवस्थित कीजिए।
उत्तर
a. यहाँ, `1/2 = 1/2 xx 11/11 = 11/22`
और `5/11 = 5/11 xx 2/2 = 10/22`
इसलिए, कागज का पुनर्नवीनीकरण `1/2` से कम है।
b. इसी प्रकार, `5/8`, `1/2 (= 4/8)` से अधिक है।
साथ ही, `2/5 = (2 xx 2)/(5 xx 2) = 4/10 < 1/2 (= 5/10)`
और `3/4 > 1/2 (= 2/4)`
इसलिए, कागज और कांच के पुनर्चक्रण की मात्रा `1/2` से कम है।
c. एल्यूमीनियम के डिब्बे की मात्रा = `5/8 (= 10/16)` से अधिक होता है `1/2` एल्यूमीनियम के डिब्बे की मात्रा
= `5/8 xx 1/2`
= `5/16`
d. 11, 8, 5, 4 का लघुत्तम समापवर्त्य लेने पर = 440
अब, `5/11 = 5/11 xx 40/40 = 200/440`
`5/8 = 5/8 xx 55/55 = 275/440`
`2/5 = 2/5 xx 88/88 = 176/440`
`3/4 = 3/4 xx 110/110 = 330/440`
जैसा कि, `330/440 > 275/440 > 200/440 > 176/440`
यानी `3/4 > 5/8 > 5/11 > 2/5`
इसका मतलब है, अन्य > एल्युमीनियम के डिब्बे > कागज़ > कांच।
APPEARS IN
संबंधित प्रश्न
परिमेय संख्या जो अपने ऋणात्मक के समान है।
`p/q` के रूप की संख्या परिमेय संख्या कहलाती है, यदि ______।
प्रत्येक परिमेय संख्या x के लिए, x + 1 = x होता है।
प्रत्येक पूर्ण संख्या एक पूर्णांक है।
नीचे दिए हुए आरेख में चिड़ियों की विभिन्न प्रजातियों के पंखों के उत्तर देने के लिए, इस आरेख का प्रयोग कीजिए –
| गोल्डन ईगल | ब्लू जय |
 |
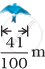 |
एक ब्लू जय के पंखों से एक गोल्डन ईगल के पंख कितने अधिक लंबे है?
कई चौड़े स्क्रीन वाले टेलीविजनों की सेंटीमीटरों में सामान्य चौड़ाइयाँ `98 4/9, 98 1/25`और 97.94 हैं। इन संख्याओं को `p/q` के रूप की परिमेय संख्याओं के रूप में व्यक्त कीजिए तथा चौड़ाइयों को आरोही क्रम में व्यवस्थित कीजिए।
कुछ राज्यों में पुरुषों के जीवन काल की औसत प्रत्याशाएँ नीचे सारणी में दर्शायी गई है। प्रत्येक दशमलव को `p/q` के रूप में व्यक्त कीजिए तथा राज्यों को सबसे कम से सबसे अधिक पुरुष जीवन काल प्रत्याशाओं के क्रम में व्यवस्थित कीजिए। राज्य अनुसार आंकड़े नीचे दिए हैं ; प्रत्येक राज्य के लिए होमपेज के "FACTFILE" खंड में अधिक सूचक ज्ञात किए जा सकते है।
| राज्य | पुरुष | `bb(p/q)` रूप | न्यूनतम रूप |
| आंध्र प्रदेश | 61.6 | ||
| असम | 57.1 | ||
| बिहार | 60.7 | ||
| गुजरात | 61.9 | ||
| हरियाणा | 64.1 | ||
| हिमाचल प्रदेश | 65.1 | ||
| कर्नाटक | 62.4 | ||
| केरल | 70.6 | ||
| मध्य प्रदेश | 56.5 | ||
| महाराष्ट्र | 64.5 | ||
| ओडिशा | 57.6 | ||
| पंजाब | 66.9 | ||
| राजस्थान | 59.8 | ||
| तमिलनाडु | 63.7 | ||
| उत्तर प्रदेश | 58.9 | ||
| पश्चिम बंगाल | 62.8 | ||
| भारत | 60.8 |
स्त्रोत ; रजिस्ट्रार जनरल ऑफ़ इंडिया (2003) की एस आर एस पर आधारित संक्षिप्त की गई सारणियाँ। एस आर एस वैश्लेषिक अध्ययन, 2003 की रिपोर्ट 3 : रजिस्ट्रार जनरल ऑफ़ इंडिया, नई दिल्ली। यह आँकड़े समय अवधि 1995 – 99 के है। बाद में, राज्य विभाजित हो गए थे, परंतु केवल वे ही इस रिपोर्ट में सम्मलित है जो विभाजन से पूर्व थे। (मध्य प्रदेश में छत्तीसगढ़, यूपी में उत्तरखंड और बिहार में झारखंड)
निम्नलिखित परिमेय संख्या को संख्या `p/q` रूप में लिखिए।
`0.bar6`
निम्नलिखित संख्या के मध्य स्थित कोई भी तीन परिमेय संख्याएँ ज्ञात कीजिए।
0.3 और -0.5
निम्नलिखित संख्या के मध्य स्थित कोई भी तीन परिमेय संख्याएँ ज्ञात कीजिए।
-2.3 और -2.33
