Advertisements
Advertisements
प्रश्न
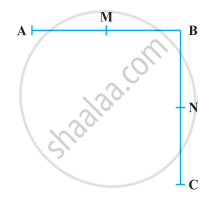
निम्नलिखित आकृति में AB = BC, M रेखाखंड AB का मध्य-बिंदु है और N रेखाखंड BC का मध्य-बिंदु है। दर्शाइए कि AM = NC है।
उत्तर
दिया गया है, AB = BC ...(i)
M, AB का मध्य-बिंदु है।
∴ AM = MB = `1/2` AB ...(ii)
और N, BC का मध्य-बिंदु है।
∴ BN = NC = `1/2` BC ...(iii)
यूक्लिड की अभिगृहीत के अनुसार, जो चीज़ें एक ही चीज़ के आधे हिस्से हैं वे एक दूसरे के बराबर हैं।
समीकरण (i) से, AB = BC
दोनों पक्षों को `1/2` से गुणा करने पर, हम पाते होता हैं।
`1/2` AB = `1/2` BC
⇒ AM = NC ...[समीकरण (ii) और (iii) का प्रयोग करके]
APPEARS IN
संबंधित प्रश्न
निम्नलिखित पद की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
रेखाखंड
नीचे दी हुई दो अभिधरणाओं पर विचार कीजिए:
- दो भिन्न बिंदु A और B दिए रहने पर, एक तीसरा बिंदु C ऐसा विद्यमान है जो A और B के बीच स्थित होता है।
- यहाँ कम से कम ऐसे तीन बिंदु विद्यमान हैं कि वे एक रेखा पर स्थित नहीं हैं।
यूक्लिड निम्नलिखित देश का वासी था :
पाइथागोरस एक विद्यार्थी था :
एक पृष्ठ के किनारे वक्र होते हैं।
वस्तुएँ जो एक ही वस्तु की दोगुनी हों परस्पर बराबर होती हैं।
यूक्लिड की पाँचवीं अभिधारणा को अन्य अभिधारणाओं और अभिगृहीतों का प्रयोग करते हुए, सिद्ध करने के प्रयासों के फलस्वरूप अन्य अनेक ज्यामितियों की खोज हुई।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
दो सेल्समैन ने अगस्त के महीने में बराबर बिक्री की। सितंबर में, प्रत्येक सेल्समैन अपनी बिक्री अगस्त के महीने की बिक्री की दोगुनी कर लेता है। दोनों की सितंबर की बिक्रियों की तुलना कीजिए।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
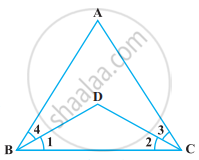
निम्नलिखित आकृति में, ∠1 = ∠3 और ∠2 = ∠4 है। दर्शाइए कि ∠A = ∠C है।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
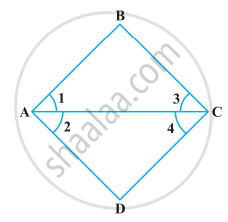
निम्नलिखित आकृति में, ∠ABC = ∠ACB और ∠3 = ∠4 है। दर्शाइए कि ∠1 = ∠2 है।