Question

निम्नलिखित असमिकाओं की ज्यामिति या किसी अन्य विधि द्वारा स्थापना कीजिए:

1. | a+b | ≤ |a| + |b|
2. |a + b| ≥ | |a| - |b| |
3. |a - b| ≤ |a| + |b|
4. |a-b| ≥ | |a| - |b| |

इनमें समिका (समता) का चिन्ह कब लागू होता है ?

Answer 1

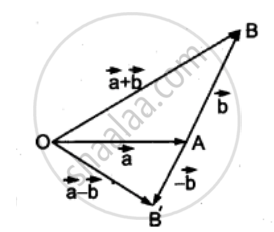
माना   `vec"a" = vec "OA"` तथा  `vec"b" = vec "AB"`

तब   `vec|"a"| = "OA"` तथा  `vec|"b"| = "AB"`

1.  सदिश योग के त्रिभुज नियम से, 
   `vec"a" + vec"b" = vec"OA" + vec"AB" = vec"OB"`
   अर्थात `vec"a" + vec"b", Δ"OAB"` 
   अर्थात की तीसरी भुजा OB द्वारा दिशा व परिमाण में निरूपित होगा।
   तथा `|vec"a" + vec"b"| = "OB"`
   ∵ ΔOAB में,  OB≤ OA + OB
   या `|vec"a" + vec"b"| ≤ |vec"a"| + |vec"b"|`
2. ∵ किसी त्रिभुज में प्रत्येक भुजा शेष दो भुजाओं के अंतर से बड़ी होती है; अतः
   OB ≥ OA - AB
   या `|vec"a" + vec"b"| ≥ |vec"a"| - |vec"b"|`     ...(1)
   तथा  OB ≥ AB - OA 
   या `|vec"a" + vec"b"| ≥ |vec"b"| - |vec"a"|`      ... (2)
   समीकरण (1) व (2) को एक साथ समायोजित करने पर,
   `|vec"a" + vec"b"| ≥ |vec"a"| - |vec"b"|`
3. माना `-vec"b" = vec"AB"` तब  AB = AB   अर्थात  `|-vec"b"| = |vec"b"| = "AB"` तब सदिश योग के त्रिभुज नियम से,
   `vec"a" - vec"b" = vec"a" + vec"(-b)"`
   = `vec"OA"  + vec"AB" = vec"OB"  => |vec"a" - vec"b"| = "OB"`
   अर्थात सदिश `vec"a" - vec"b"`, ΔOAB की भुजा OB जब से निरूपित होगा।
   ΔOAB में OB ≤ OA + AB
   अर्थात `|vec"a" - vec"b"| ≤ |vec"a"| + |vec"-b"|`
   या `|vec"a" - vec"b"| ≤ |vec"a"| + |vec"b"|`
4. ∵ किसी त्रिभुज में प्रत्येक भुजा शेष दो भुजाओं के अंतर से बड़ी होती है |
   ∴ OB = OA - AB   ....(1)
   या `|vec"a" - vec"b"| ≥ |vec"b"| - |vec"a"|` (∵AB = `|vec"-b"| = |vec"b"|`)
   तथा OB≥ AB - OA
   या `|vec"a" - vec"b"| ≥ |vec"b"| - |vec"a"|` ......(2)
   समीकरण (1) व (2) को एक साथ समायोजित करने पर,
5. `|vec"a" - vec"b"| ≥ |vec"a"| - |vec"b"|`
   उपर्युक्त सभी में समीका का चिन्ह केवल तभी लागू होगा जबकि सदिश `vec"a"` व `vec"b"` समदिश होंगे।