Advertisements
Advertisements
प्रश्न
O केंद्र असलेल्या वर्तुळाची AB जीवा आहे. AOC वर्तुळाचा व्यास आहे. स्पर्शिका AT वर्तुळाला बिंदू A मध्ये स्पर्श करते.
खालील प्रश्नांची उत्तरे लिहा:
- वरील दिलेल्या माहितीवरून आकृती काढा.
- ∠CAT व ∠ABC ची मापे काढा व त्याचे कारण लिहा.
- ∠CAT व ∠ABC एकरूप आहेत का? स्पष्टीकरण लिहा.
उत्तर

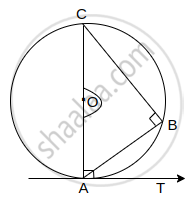
∠CAT = ∠OAT = 90° .....(स्पर्शिकेनुसार)
∠ABC = 90° ......(अर्धवर्तुळातील कोन काटकोन असतो.)- ∠CAT = ∠ABC
∠CAT ≅ ∠ABC ......[∴ वर्तुळाची स्पर्शिका व स्पर्शबिंदूतून काढलेली जीवा यांतील कोन त्या कोनाने अंतर्खंडित केलेल्या कंसाच्या विरुद्ध कंसात अंतर्लिखित केलेल्या कोनाएवढा असतो.]
APPEARS IN
संबंधित प्रश्न
प्रत्येक उपप्रश्नासाठी चार पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक पर्याय निवडा.
परस्परांना छेदणाऱ्या दोन वर्तुळांपैकी प्रत्येक वर्तुळ दुसऱ्या वर्तुळाच्या केंद्रातून जाते. जर त्यांच्या केंद्रांतील अंतर 12 सेमी असेल, तर प्रत्येक वर्तुळाची त्रिज्या किती सेमी आहे?
प्रत्येक उपप्रश्नासाठी चार पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक पर्याय निवडा.
‘एक वर्तुळ एका समांतरभुज चौकोनाच्या सर्व बाजूंना स्पर्श करते, तर तो समांतरभुज चौकोन ______ असला पाहिजे’, या विधानातील रिकाम्या जागी योग्य शब्द लिहा.
सोबतच्या आकृतीत, केंद्र X आणि Y असलेली वर्तुळे परस्परांना बिंदू Z मध्ये स्पर्श करतात. बिंदू Z मधून जाणारी वृत्तछेदिका त्या वर्तुळांना अनुक्रमे बिंदू A व बिंदू B मध्ये छेदते. तर सिद्ध करा, त्रिज्या XA || त्रिज्या YB. खाली दिलेल्या सिद्धतेतील रिकाम्या जागा भरून पूर्ण सिद्धता लिहून काढा.
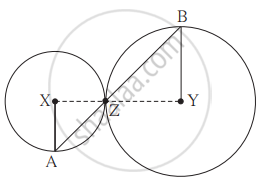
रचना : रेख XZ आणि ______ काढले.
सिद्धता : स्पर्शवर्तुळांच्या प्रमेयानुसार, बिंदू X, Z, Y हे ______ आहेत.
∴ ∠XZA ≅ ______ विरुद्ध कोन
∠XZA = ∠BZY = a मानू ______ (I)
आता, रेख XA ≅ रेख XZ ______(______)
∴ ∠XAZ = ______ = a ______ (समद्विभुज त्रिकोणाचे प्रमेय) (II)
तसेच रेख YB ≅ ______ ______(______)
∴ ∠BZY = ______ = a ______(______) (III)
∴ (I), (II) व (III) वरून,
∠XAZ = ______
∴ त्रिज्या XA || त्रिज्या YB ______(______)
वर्तुळाचे कोणतेही तीन बिंदू एकरेषीय नसतात, हे सिद्ध करा.
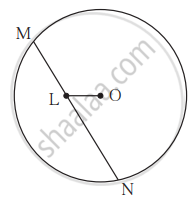
सोबतच्या आकृतीत रेख MN ही केंद्र O असलेेल्या वर्तुळातील जीवा आहे. MN = 25, जीवा MN वर बिंदू L असा आहे की ML = 9 आणि d(O,L) = 5 तर या वर्तुळाची त्रिज्या किती असेल?
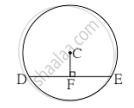
सोबतच्या आकृतीमध्ये, केंद्र C असलेल्या वर्तुळाची रेख DE ही जीवा आहे. रेख CF ⊥ जीवा DE आणि DE = 16 सेमी, तर DF ची लांबी काढा.
सोबतच्या आकृतीत, केंद्र A असलेल्या वर्तुळाला रेषा MN बिंदू M मध्ये स्पर्श करते. जर AN = 13 तसेच MN = 5 असेल, तर वर्तुळाची त्रिज्या काढा.

एका वर्तुळाच्या केंद्रापासून 15 सेमी अंतरावरील एका बिंदूतून त्या वर्तुळाला काढलेल्या स्पर्शिकाखंडाची लांबी 12 सेमी असेल, तर त्या वर्तुळाचा व्यास काढा.
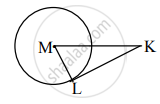
सोबतच्या आकृतीत, बिंदू M वर्तुळ केंद्र आणि रेख KL हा स्पर्शिकाखंड आहे. जर MK = 12, KL = `6sqrt3`, तर
- वर्तुळाची त्रिज्या काढा.
- ∠K आणि ∠M
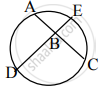
आकृतीमध्ये, जीवा AC आणि जीवा DE बिंदू B मध्ये छेदतात. जर ∠ABE = 100° आणि m(कंस AE) = 95°, तर m(कंस DC) काढा.