Question

Obtain a relation for the magnetic induction at a point along the axis of a circular coil carrying current.

Answer 1

Consider a current carrying circular loop of radius R and let I be the current flowing through the wire in the direction. The magnetic field at a point P on the axis of the circular coil at a distance z from its center of the coil O. It is computed by taking two diametrically opposite line elements of the coil each of length `vec"dl"` at C and D. Let `vec"r"` be the vector joining the current element `(1vec"dl")` at C to the point P.

PC = PD = T = `sqrt("R"^2 + "Z"^2)` and

angle ∠CPO = ∠DPO = θ

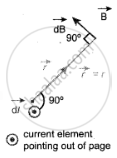
According to Biot-Savart’s law, the magnetic field at P due to the current element `l vec"dl"` is

`"d"vec"B" = mu_0/(4pi) = ("I"vec"dl" xx hat"r")/"r"^2`    .....(1)

The magnitude of the magnetic field due to current element l dl at C and D are equal because of equal distance from the coil. The magnetic field dB due to each current element I `vec"dl"` is resolved into two components; dB sin θ along y-direction and dB cos θ along z-direction. Horizontal components of each current element cancel out while the vertical components (dB cos θ k^) alone contribute to a total magnetic field at the point P.

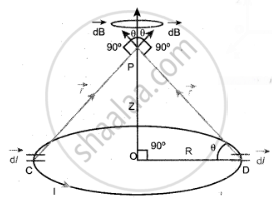
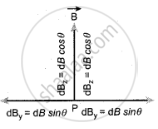
If we integrate `vec"dl"` around the loop, `"d"vec"B"` sweeps out a cone, then the net magnetic field `vec"B"` at point P is

`vec"B" = int "d"bec"B" = int "dB"cos theta hat"k"`     ....(2)

`vec"B" = (mu_0"I")/(4pi) int "dl"/"r"^2 cos theta hat"k"`    ....(3)

But cos θ = `"R"/("R"^2 + "Z"^2)^(1/2)`

Using Pythagorous theorem r² = R² + Z² and integrating line element from 0 to 2πR, we get

`vec"B" = (mu_0"I")/(2pi) "R"^2/("R"^2 + "Z"^2)^(3/2) hat"k"`  ....(4)

Note that the magnetic field `vec"B"` points along the direction from the point O to P. Suppose if the current flows in a clockwise direction, then magnetic field points in the direction from the point P to O.