Advertisements
Advertisements
प्रश्न
Obtain an expression for potential energy due to a collection of three point charges which are separated by finite distances.
उत्तर
Electrostatic potential energy for a collection of point charges:
The electric potential at a point at a distance r from point charge ql is given by
V = `1/(4piε_0) "q"_1/"r"` ....(1)
This potential V is the work done to bring a unit positive charge from infinity to the point. Now if the charge q2 is brought from infinity to that point at a distance r from qp the work done is the product of q2 and the electric potential at that point. Thus we have W = q2V …… (2)
This work done is stored as the electrostatic potential energy U of a system of charges q1 and q2 separated by a distance r. Thus we have
U = `"q"_2"V" = 1/(4piε_0) ("q"_1"q"_2)/"r"` ....(3)
The electrostatic potential energy depends only on the distance between the two point charges. In fact, the expression (3) is derived by assuming that q1 is fixed and q2 is brought from infinity. The equation (3) holds true when q2 is fixed and q1 is brought from infinity or both q2and q2 are simultaneously brought from infinity to a distance r between them.
Three charges are arranged in the following configuration as shown in Figure.
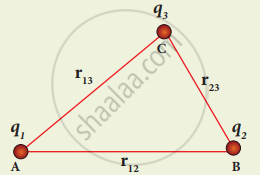
Electrostatic potential energy for collection of point charges
To calculate the total electrostatic potential energy, we use the following procedure. We bring all the charges one by one and arrange them according to the configuration.
-
Bringing a charge q1 from infinity to the point A requires no work, because there are no other charges already present in the vicinity of charge q1
- To bring the second charge q2 to the point B, work must be done against the electric field created by the charge q1 So the work done on the charge q1 is W = q2V1B. Here V1B is the electrostatic potential due to the charge q1 at point B.
U = `1/(4 pi ε_0) ("q"_1"q"_2)/"r"_12` .....(4)
Note that the expression is same when q2 is brought first and then q1 later.
- Similarly to bring the charge q3 to the point C, work has to be done against the total electric field due to both charges q1 and q2. So the work done to bring the charge q3 is = q3 (V1C + V2C). Here V1C is the electrostatic potential due to charge q1 at point C and V2C is the electrostatic potential due to charge q2 at point C. The electrostatic potential is
U = `1/(4 pi ε_0) (("q"_1"q"_3)/"r"_13 + ("q"_2"q"3)/"r"_23)` ....(5) - Adding equations (4) and (5), the total electrostatic potential energy for the system of three charges q1,q2 and q3 is
U = `1/(4 pi ε_0) (("q"_1"q"_2)/"r"_12 + ("q"_1"q"3)/"r"_13 + ("q"_2"q"_3)/"r"_23)` ....(6)
Note that this stored potential energy U is equal to the total external work done to assemble the three charges at the given locations. The expression (6) is same if the charges are brought to their positions in any other order. Since the Coulomb force is a conservative force, the electrostatic potential energy is independent of the manner in which the configuration of charges is arrived at.
APPEARS IN
संबंधित प्रश्न
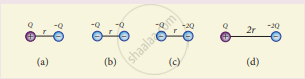
Rank the electrostatic potential energies for the given system of charges in increasing order.
An electric field `vec"E" = 10 xx hat"i"` exists in a certain region of space. Then the potential difference V = Vo – VA, where Vo is the potential at the origin and VA is the potential at x = 2 m is:
Give the relation between electric field and electric potential.
Derive an expression for electrostatic potential due to a point charge.
Derive an expression for electrostatic potential due to an electric dipole.
The total number of electrons in the human body is typically in the order of 1028. Suppose, due to some reason, you and your friend lost 1% of this number of electrons. Calculate the electrostatic force between you and your friend separated at a distance of lm. Compare this with your weight. Assume the mass of each person is 60kg and use point charge approximation.
Draw the free body diagram for the following charges as shown in the following figure.
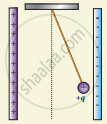
Draw the free body diagram for the following charges as shown in the following figure.

A spark plug in a bike or a car is used to ignite the air-fuel mixture in the engine. It consists of two electrodes separated by a gap of around 0.6 mm gap as shown in the figure.

To create the spark, an electric field of magnitude 3 x 106Vm-1 is required,
- What potential difference must be applied to produce the spark?
- If the gap is increased, does the potential difference increase, decrease or remains the same?
- Find the potential difference if the gap is 1 mm.
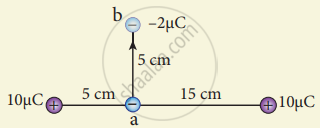
A point charge of +10 µC is placed at a distance of 20 cm from another identical point charge of +10 µC. A point charge of -2 µC is moved from point a to b as shown in the figure. Calculate the change in potential energy of the system? Interpret your result.