Advertisements
Advertisements
प्रश्न
Derive an expression for electrostatic potential due to an electric dipole.
उत्तर
Consider two equal and opposite charges separated by a small distance 2a. The point P is located at a distance r from the midpoint of the dipole. Let θ be the angle between the line OP and dipole axis AB.
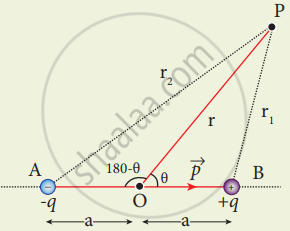
Potential due to electric dipole
Let r1 be the distance of point P from +q and r2 be the distance of point P from -q.
Potential at P due to charge +q = `1/(4 pi ε_0) "q"/"r"_1`
Potential at P due to charge –q = `−1/(4 pi ε_0) "q"/"r"_1`
Total potential at the point P
V = `1/(4 pi ε_0) "q"(1/"r"_1 - 1/"r"_2)`
By the cosine law for triangle BOP
r12 =r2 + a2 – 2ra cos θ
`"r"_1^2 = "r"^2 (1 + "a"^2/"r"^2 - "2a"/"r" cos theta)`
`"a"^2/"r"^2` is very small, and can be neglected.
`"r"_1^2 = "r"^2(1 - "2a" (cos theta)/"r")` (or)
`"r"_1 = "r"(1 - "2a"/"r" cos theta)^2`
`1/"r"_1 = 1/"r" (1 - "2a"/"r" cos theta)^(-1/2)`
Since `"a"/"r"` << 1, we can use binomial theorem and retain the terms up to first order
`1/"r"_1 = 1/"r" (1 + "a"/"r" cos theta)` ....(2)
Similarly applying the cosine law for triangle A0P,
r22 = r2 + a2 – 2racos(180-θ)
since cos(180-θ) = – cos θ
r22 = r2 + a2 +2ra cos θ
Neglecting `"a"^2/"r"^2 "r"^_2 = "r"^2 (1 + (2"a" cos theta)/"r")`
`"r"_2 = "r" (1 + (2"a" cos theta)/"r")^(1/2)`
Using Binomial theorem, we get
`1/"r"_2 = 1/"r" (1 - "a" (cos theta)/"r")` ....(3)
Sun (2) and (3) in eqn (1), we get
V = `"q"/(4piε_0) (1/"r"(1 + "a"(cos theta)/"r") - 1/"r" (1 - "a" (cos theta)/"r"))`
V = `"q"/(4piε_0) (1/"r"(1 + "a" (cos theta)/"r" - 1 + "a" (cos theta)/"r"))`
V = `1/(4piε_0) (2"aq")/"r"^2 cos theta`
But the electric dipole moment p = 2qa and we get,
V = `1/(4piε_0) (("p" cos theta)/"r"^2)`
p cos θ = `vec"p" * hat"r"`, where `hat "r"` is the unit vector from the point O to point P.
V = `1/(4piε_0) ((vec"p" * hat"r")/"r"^2)`
Special Cases:
| If the point lies near | θ | V |
| +q | O° | `"p"/(4 piε_0"r"^2)` |
| -q | 180° | -`"p"/(4 piε_0"r"^2)` |
| equatorial point | 90° | 0 |
APPEARS IN
संबंधित प्रश्न
A thin conducting spherical shell of radius R has a charge Q which is uniformly distributed on its surface. The correct plot for electrostatic potential due to this spherical shell is
Two points A and B are maintained at a potential of 7 V and -4 V respectively. The work done in moving 50 electrons from A to B is ______.
Give the relation between electric field and electric potential.
Define ‘electrostatic potential energy’.
Derive an expression for electrostatic potential energy of the dipole in a uniform electric field.
The total number of electrons in the human body is typically in the order of 1028. Suppose, due to some reason, you and your friend lost 1% of this number of electrons. Calculate the electrostatic force between you and your friend separated at a distance of lm. Compare this with your weight. Assume the mass of each person is 60kg and use point charge approximation.
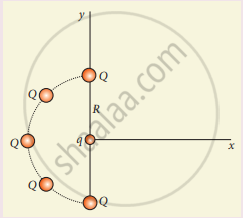
Five identical charges Q are placed equidistant on a semicircle as shown in the figure. Another point charge q is kept at the center of the circle of radius R. Calculate the electrostatic force experienced by the charge q.
Suppose a charge +q on Earth’s surface and another +q charge is placed on the surface of the Moon,
- Calculate the value of q required to balance the gravitational attraction between Earth and Moon
- Suppose the distance between the Moon and Earth is halved, would the charge q change?
(Take mE = 5.9 x 1024 kg, mM = 7.348 x 1022 kg)
Draw the free body diagram for the following charges as shown in the following figure.

A spark plug in a bike or a car is used to ignite the air-fuel mixture in the engine. It consists of two electrodes separated by a gap of around 0.6 mm gap as shown in the figure.

To create the spark, an electric field of magnitude 3 x 106Vm-1 is required,
- What potential difference must be applied to produce the spark?
- If the gap is increased, does the potential difference increase, decrease or remains the same?
- Find the potential difference if the gap is 1 mm.
