Advertisements
Advertisements
प्रश्न
Derive an expression for electrostatic potential due to an electric dipole.
उत्तर
Consider two equal and opposite charges separated by a small distance 2a. The point P is located at a distance r from the midpoint of the dipole. Let θ be the angle between the line OP and dipole axis AB.
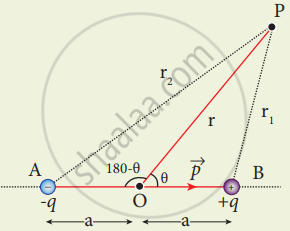
Potential due to electric dipole
Let r1 be the distance of point P from +q and r2 be the distance of point P from -q.
Potential at P due to charge +q = `1/(4 pi ε_0) "q"/"r"_1`
Potential at P due to charge –q = `−1/(4 pi ε_0) "q"/"r"_1`
Total potential at the point P
V = `1/(4 pi ε_0) "q"(1/"r"_1 - 1/"r"_2)`
By the cosine law for triangle BOP
r12 =r2 + a2 – 2ra cos θ
`"r"_1^2 = "r"^2 (1 + "a"^2/"r"^2 - "2a"/"r" cos theta)`
`"a"^2/"r"^2` is very small, and can be neglected.
`"r"_1^2 = "r"^2(1 - "2a" (cos theta)/"r")` (or)
`"r"_1 = "r"(1 - "2a"/"r" cos theta)^2`
`1/"r"_1 = 1/"r" (1 - "2a"/"r" cos theta)^(-1/2)`
Since `"a"/"r"` << 1, we can use binomial theorem and retain the terms up to first order
`1/"r"_1 = 1/"r" (1 + "a"/"r" cos theta)` ....(2)
Similarly applying the cosine law for triangle A0P,
r22 = r2 + a2 – 2racos(180-θ)
since cos(180-θ) = – cos θ
r22 = r2 + a2 +2ra cos θ
Neglecting `"a"^2/"r"^2 "r"^_2 = "r"^2 (1 + (2"a" cos theta)/"r")`
`"r"_2 = "r" (1 + (2"a" cos theta)/"r")^(1/2)`
Using Binomial theorem, we get
`1/"r"_2 = 1/"r" (1 - "a" (cos theta)/"r")` ....(3)
Sun (2) and (3) in eqn (1), we get
V = `"q"/(4piε_0) (1/"r"(1 + "a"(cos theta)/"r") - 1/"r" (1 - "a" (cos theta)/"r"))`
V = `"q"/(4piε_0) (1/"r"(1 + "a" (cos theta)/"r" - 1 + "a" (cos theta)/"r"))`
V = `1/(4piε_0) (2"aq")/"r"^2 cos theta`
But the electric dipole moment p = 2qa and we get,
V = `1/(4piε_0) (("p" cos theta)/"r"^2)`
p cos θ = `vec"p" * hat"r"`, where `hat "r"` is the unit vector from the point O to point P.
V = `1/(4piε_0) ((vec"p" * hat"r")/"r"^2)`
Special Cases:
| If the point lies near | θ | V |
| +q | O° | `"p"/(4 piε_0"r"^2)` |
| -q | 180° | -`"p"/(4 piε_0"r"^2)` |
| equatorial point | 90° | 0 |
APPEARS IN
संबंधित प्रश्न
Which charge configuration produces a uniform electric field?
A thin conducting spherical shell of radius R has a charge Q which is uniformly distributed on its surface. The correct plot for electrostatic potential due to this spherical shell is
Two points A and B are maintained at a potential of 7 V and -4 V respectively. The work done in moving 50 electrons from A to B is ______.
What is an equipotential surface?
Define ‘electrostatic potential energy’.
Obtain an expression for potential energy due to a collection of three point charges which are separated by finite distances.
Five identical charges Q are placed equidistant on a semicircle as shown in the figure. Another point charge q is kept at the center of the circle of radius R. Calculate the electrostatic force experienced by the charge q.
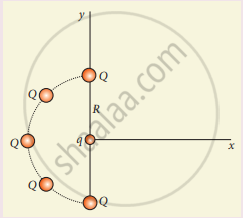
Draw the free body diagram for the following charges as shown in the following figure.
Draw the free body diagram for the following charges as shown in the following figure.

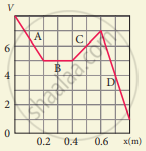
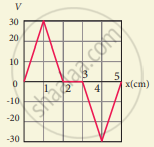
The electrostatic potential is given as a function of x in figure (a) and (b). Calculate the corresponding electric fields in regions A, B, C and D. Plot the electric field as a function of x for figure (b).