Advertisements
Advertisements
प्रश्न
Derive an expression for electrostatic potential due to a point charge.
उत्तर
- Consider a positive charge ‘q’ kept fixed at the origin. Let P be a point at distance r from the charge ‘q’.
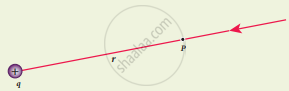
Electrostatic potential at a point P - The electric potential at the point P is
V = `int_∞^"r" (- vec"E")* "d"vec"r" = - int_∞^"r" vec"E" * vec"dr"` - Electric field due to positive point charge is
`vec"E" = 1/(4piε_0) "q"/"r"^2 hat"r"`
V = `- 1/(4piε_0) int_∞^"r" "q"/"r"^2 hat"r" * "d" vec"r"` - The infinitesimal displacement vector,
`"d"vec"r" = "dr" hat"r"` and using `hat "r" hat "r"` = 1, we have
V = `- 1/(4piε_0) int_∞^"r" "q"/"r"^2 hat"r" * "dr" hat"r" = - 1/(4piε_0) int_∞^"r" "q"/"r"^2 "dr"` - After the integration,
V = `- 1/(4piε_0) "q"{- 1/"r"}_∞^"r" = 1/(4piε_0) "q"/"r"` - Hence the electric potential due to a point charge q at a distance r is
V = `1/(4piε_0) "q"/"r"`
APPEARS IN
संबंधित प्रश्न
Which charge configuration produces a uniform electric field?
An electric field `vec"E" = 10 xx hat"i"` exists in a certain region of space. Then the potential difference V = Vo – VA, where Vo is the potential at the origin and VA is the potential at x = 2 m is:
A thin conducting spherical shell of radius R has a charge Q which is uniformly distributed on its surface. The correct plot for electrostatic potential due to this spherical shell is
What is an equipotential surface?
What is meant by electrostatic energy density?
Suppose a charge +q on Earth’s surface and another +q charge is placed on the surface of the Moon,
- Calculate the value of q required to balance the gravitational attraction between Earth and Moon
- Suppose the distance between the Moon and Earth is halved, would the charge q change?
(Take mE = 5.9 x 1024 kg, mM = 7.348 x 1022 kg)
Draw the free body diagram for the following charges as shown in the following figure.
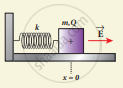
Draw the free body diagram for the following charges as shown in the following figure.
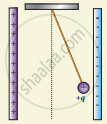
Draw the free body diagram for the following charges as shown in the following figure.

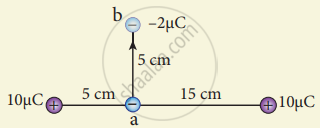
A point charge of +10 µC is placed at a distance of 20 cm from another identical point charge of +10 µC. A point charge of -2 µC is moved from point a to b as shown in the figure. Calculate the change in potential energy of the system? Interpret your result.