Advertisements
Advertisements
Question
Derive an expression for electrostatic potential due to an electric dipole.
Solution
Consider two equal and opposite charges separated by a small distance 2a. The point P is located at a distance r from the midpoint of the dipole. Let θ be the angle between the line OP and dipole axis AB.
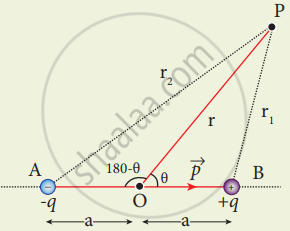
Potential due to electric dipole
Let r1 be the distance of point P from +q and r2 be the distance of point P from -q.
Potential at P due to charge +q = `1/(4 pi ε_0) "q"/"r"_1`
Potential at P due to charge –q = `−1/(4 pi ε_0) "q"/"r"_1`
Total potential at the point P
V = `1/(4 pi ε_0) "q"(1/"r"_1 - 1/"r"_2)`
By the cosine law for triangle BOP
r12 =r2 + a2 – 2ra cos θ
`"r"_1^2 = "r"^2 (1 + "a"^2/"r"^2 - "2a"/"r" cos theta)`
`"a"^2/"r"^2` is very small, and can be neglected.
`"r"_1^2 = "r"^2(1 - "2a" (cos theta)/"r")` (or)
`"r"_1 = "r"(1 - "2a"/"r" cos theta)^2`
`1/"r"_1 = 1/"r" (1 - "2a"/"r" cos theta)^(-1/2)`
Since `"a"/"r"` << 1, we can use binomial theorem and retain the terms up to first order
`1/"r"_1 = 1/"r" (1 + "a"/"r" cos theta)` ....(2)
Similarly applying the cosine law for triangle A0P,
r22 = r2 + a2 – 2racos(180-θ)
since cos(180-θ) = – cos θ
r22 = r2 + a2 +2ra cos θ
Neglecting `"a"^2/"r"^2 "r"^_2 = "r"^2 (1 + (2"a" cos theta)/"r")`
`"r"_2 = "r" (1 + (2"a" cos theta)/"r")^(1/2)`
Using Binomial theorem, we get
`1/"r"_2 = 1/"r" (1 - "a" (cos theta)/"r")` ....(3)
Sun (2) and (3) in eqn (1), we get
V = `"q"/(4piε_0) (1/"r"(1 + "a"(cos theta)/"r") - 1/"r" (1 - "a" (cos theta)/"r"))`
V = `"q"/(4piε_0) (1/"r"(1 + "a" (cos theta)/"r" - 1 + "a" (cos theta)/"r"))`
V = `1/(4piε_0) (2"aq")/"r"^2 cos theta`
But the electric dipole moment p = 2qa and we get,
V = `1/(4piε_0) (("p" cos theta)/"r"^2)`
p cos θ = `vec"p" * hat"r"`, where `hat "r"` is the unit vector from the point O to point P.
V = `1/(4piε_0) ((vec"p" * hat"r")/"r"^2)`
Special Cases:
| If the point lies near | θ | V |
| +q | O° | `"p"/(4 piε_0"r"^2)` |
| -q | 180° | -`"p"/(4 piε_0"r"^2)` |
| equatorial point | 90° | 0 |
APPEARS IN
RELATED QUESTIONS
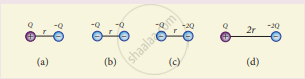
Rank the electrostatic potential energies for the given system of charges in increasing order.
What are the properties of an equipotential surface?
Give the relation between electric field and electric potential.
Obtain an expression for potential energy due to a collection of three point charges which are separated by finite distances.
Derive an expression for electrostatic potential energy of the dipole in a uniform electric field.
The total number of electrons in the human body is typically in the order of 1028. Suppose, due to some reason, you and your friend lost 1% of this number of electrons. Calculate the electrostatic force between you and your friend separated at a distance of lm. Compare this with your weight. Assume the mass of each person is 60kg and use point charge approximation.
Suppose a charge +q on Earth’s surface and another +q charge is placed on the surface of the Moon,
- Calculate the value of q required to balance the gravitational attraction between Earth and Moon
- Suppose the distance between the Moon and Earth is halved, would the charge q change?
(Take mE = 5.9 x 1024 kg, mM = 7.348 x 1022 kg)
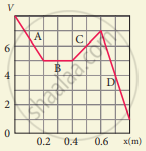
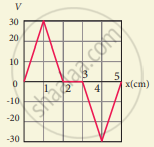
The electrostatic potential is given as a function of x in figure (a) and (b). Calculate the corresponding electric fields in regions A, B, C and D. Plot the electric field as a function of x for figure (b).
A spark plug in a bike or a car is used to ignite the air-fuel mixture in the engine. It consists of two electrodes separated by a gap of around 0.6 mm gap as shown in the figure.

To create the spark, an electric field of magnitude 3 x 106Vm-1 is required,
- What potential difference must be applied to produce the spark?
- If the gap is increased, does the potential difference increase, decrease or remains the same?
- Find the potential difference if the gap is 1 mm.
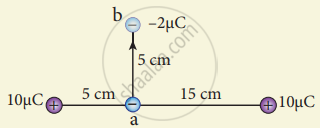
A point charge of +10 µC is placed at a distance of 20 cm from another identical point charge of +10 µC. A point charge of -2 µC is moved from point a to b as shown in the figure. Calculate the change in potential energy of the system? Interpret your result.