Advertisements
Advertisements
Question
Derive an expression for electrostatic potential energy of the dipole in a uniform electric field.
Solution
Consider a dipole placed a torque when kept in a uniform electric field `vec"E".` A dipole experiences a torque when kept in a uniform electric field `vec"E".` This torque rotates the dipole to align it with the direction of the electric field. To rotate the dipole (at constant angular velocity) from its initial angle θ’ to another angle θ against the torque exerted by the electric field, an equal and opposite external torque must be applied on the dipole.

The dipole in a uniform electric field
The work done by the external torque to rotate the dipole from angle θ’ to θ at constant angular velocity is
W = `int_(theta')^theta tau_"ext" "d"theta` ....(1)
Since τext is equal and opposite to τE = `vec"P" xx vec"E"`, we have
`|vec"r"_"ext"| = |vec"r"_"E"| = |vec"P" xx vec"E"|` ....(2)
Substituting equation (2) in equation (1) We get,
W = `int_(theta')^theta "pE sin"theta "d" theta = "pE" (cos theta' - cos theta)`
This work done is equal to the potential energy difference between the angular positions θ and θ’.
U(θ) – (Uθ’) = AU = -pE cos θ +PE cos θ’.
If the initial angle is = θ’ = 90° and is taken as reference point, then U(θ’) + pE cos θ’ = θ.
The potential energy stored in the system of dipole kept in the uniform electric field is given by El = -pE cos θ = `- vec"P"*vec"E"` ....(3)
In addition to p and E, the potential energy also depends on the orientation θ of the electric dipole with respect to the external electric field.
The potential energy is maximum when the dipole is aligned anti-parallel (θ = π) to the external electric field and minimum when the dipole is aligned parallel (θ = 0) to the external electric field.
APPEARS IN
RELATED QUESTIONS
Which charge configuration produces a uniform electric field?
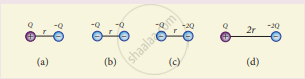
Rank the electrostatic potential energies for the given system of charges in increasing order.
Define electrostatic potential.
Give the relation between electric field and electric potential.
What is meant by electrostatic energy density?
Obtain an expression for potential energy due to a collection of three point charges which are separated by finite distances.
The total number of electrons in the human body is typically in the order of 1028. Suppose, due to some reason, you and your friend lost 1% of this number of electrons. Calculate the electrostatic force between you and your friend separated at a distance of lm. Compare this with your weight. Assume the mass of each person is 60kg and use point charge approximation.
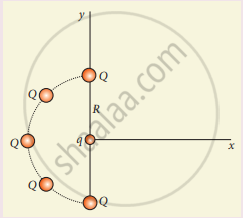
Five identical charges Q are placed equidistant on a semicircle as shown in the figure. Another point charge q is kept at the center of the circle of radius R. Calculate the electrostatic force experienced by the charge q.
Draw the free body diagram for the following charges as shown in the following figure.
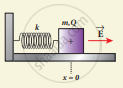
Draw the free body diagram for the following charges as shown in the following figure.

