Advertisements
Advertisements
Question
The total number of electrons in the human body is typically in the order of 1028. Suppose, due to some reason, you and your friend lost 1% of this number of electrons. Calculate the electrostatic force between you and your friend separated at a distance of lm. Compare this with your weight. Assume the mass of each person is 60kg and use point charge approximation.
Solution
Number of electrons in the human body = 1028
Number of electrons in me and my friend after lost of 1% = 1028 x 1%
`= 10^28 xx 1/100`
n = 1026 electrons
Separation distance d = 1 m
Charge of each person q = 1026 x 1.6 x 10-19
q = 1.6 x 107 C
Electrostatic force, F = `1/(4 pi epsilon_0) = ("q"_1"q"_2)/"r"^2 = (9 xx 10^9 xx 1.6 xx 10^7 xx 1.6 xx 10^7)/1^2`
F = 2.304 x 1024N
Mass of the person, M = 60 kg
Acceleration due to gravity, g = 9.8 ms-2
Weight (W) = mg
= 60 x 9.8
W = 588 N
Electrostatic force is equal to 3.92 x 1021 times of weight of the person.
APPEARS IN
RELATED QUESTIONS
An electric field `vec"E" = 10 xx hat"i"` exists in a certain region of space. Then the potential difference V = Vo – VA, where Vo is the potential at the origin and VA is the potential at x = 2 m is:
A thin conducting spherical shell of radius R has a charge Q which is uniformly distributed on its surface. The correct plot for electrostatic potential due to this spherical shell is
Two points A and B are maintained at a potential of 7 V and -4 V respectively. The work done in moving 50 electrons from A to B is ______.
Define electrostatic potential.
Give the relation between electric field and electric potential.
What is meant by electrostatic energy density?
Derive an expression for electrostatic potential due to a point charge.
Derive an expression for electrostatic potential due to an electric dipole.
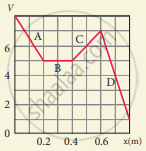
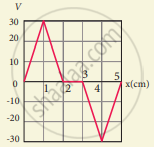
The electrostatic potential is given as a function of x in figure (a) and (b). Calculate the corresponding electric fields in regions A, B, C and D. Plot the electric field as a function of x for figure (b).
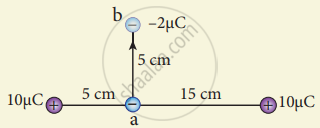
A point charge of +10 µC is placed at a distance of 20 cm from another identical point charge of +10 µC. A point charge of -2 µC is moved from point a to b as shown in the figure. Calculate the change in potential energy of the system? Interpret your result.