Advertisements
Advertisements
प्रश्न
Obtain an expression for the induced e.m.f. in a coil rotating with uniform angular velocity in
uniform magnetic field. Plot a graph of variation of induced e.m.f. against phase (Θ = ωt) over one cycle.
उत्तर
a) Consider a rectangular loop of conducting wire ‘PQRS’ partly placed in uniform
magnetic field of induction ‘B’ as shown in figure.
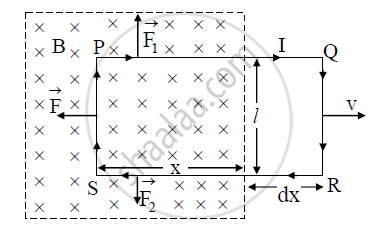
b) Let ‘l’ be the length of the side PS and ‘x’ be the length of the loop within the field.
∴ A = lx = area of the loop, which lies inside the field.
c) The magnetic flux (φ) through the area A at certain time ‘t’ is Φ = BA = Blx
d) The loop is pulled out of the magnetic field of induction ‘B’ to the right with a uniform
velocity ‘v’.
e) The rate of change of magnetic flux is given by, `(dphi)/(dt) = d/dt (Blx)`
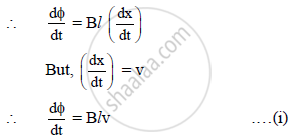
f) Due to change in magnetic flux, induced current is set up in the coil. The direction of
this current is clockwise according to Lenz’s law. Due to this, the sides of the coil
experience the forces, F1, F2 and F as shown in figure. The directions of these forces is
given by Fleming’s left hand rule.
g) The magnitude of force ‘F’ acting on the side PS is given by, F = BIl.
h) The force `vecF_1` and `vecF_2` are equal in magnitude and opposite in direction, therefore they cancel out. The only unbalanced force which opposes the motion of the coil is `vecF` Hence, work must be done against this force in order to pull the coil.
i) The work done in time ‘dt’ during the small displacement ‘dx’ is given by, dW = −Fdx
− ve sign shows that F and ‘dx’ are opposite to each other.
∴ dW = − (BIl) dx ….(ii)
j) Mechanical power is given by,

k) This external work provides the energy needed to maintain the induced current I
through the loop (coil).
l. If ‘e’ is the e.m.f induced then,
electric power = `(dW)/(dt) = eI`
∴ dW = eIdt .…(iii)
m) From equations (ii) and (iii), we have, eIdt = − BIl dx
:. `e = -Bl (dx)/(dt)`
:. e = - B/v ...(iv)
n. From equation (i) and (iv), we have,
`e =- (dphi)/(dt)`
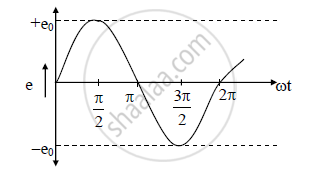
o) Graph of variation of induced e.m.f. against phase (θ = ωt) over one cycle
APPEARS IN
संबंधित प्रश्न
Obtain an expression for e.m.f. induced in a coil rotating with uniform angular velocity in a uniform magnetic field. Show graphically the variation of e.m.f. with time (t).
Resistance of a potentiometer wire is 0.1Ω/cm. A cell of e.m.f 1.5V is balanced at 300 cm on this potentiometer wire. Calculate the current and balancing length for another cell of e.m.f. 1.4V on the same potentiometer wire.
A coil of 100 turns, each of area 0.02m2 is kept in a uniform field of induction 3.5 x10-5 T. If the coil rotates with a speed of 6000 r.p.m. about an axis in the plane of the coil and perpendicular to the magnetic induction, calculate peak value of e.m.f. induced in the coil.
At which position of the plane of the rotating coil with the direction of magnetic field, the e.m.f. induced in the coil is maximum?
