Question

Obtain an expression for e.m.f. induced in a coil rotating with uniform angular velocity in a uniform magnetic field. Show graphically the variation of e.m.f. with time (t).

Resistance of a potentiometer wire is 0.1Ω/cm. A cell of e.m.f 1.5V is balanced at 300 cm on this potentiometer wire. Calculate the current and balancing length for another cell of e.m.f. 1.4V on the same potentiometer wire.

Answer 1

Coil rotating in uniform magnetic field:

Consider a coil of ‘N’ turns with effective area NA placed in uniform magnetic induction B as shown in the figure below.

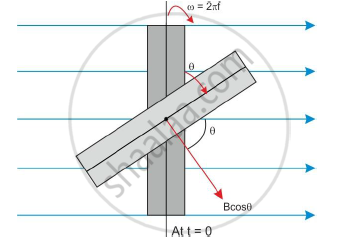
The coil is rotated continuously with constant angular velocity ω. The axis of rotation is in the plane of the coil and normal to the magnetic induction B.

At t = 0, the plane of the coil is perpendicular to the magnetic induction B.

The magnetic flux passing through the coil is NAB.

After t seconds, the plane of the coil is at an angle θ.

Thus, the magnetic flux Φ through the coil at time t is given by

       Φ = NABcosθ = NABcosωt

As time changes, the magnetic flux goes on changing. Hence, the e.m.f. generated in the coil is given by

`e=-(dphi)/(dt)=-d/dt(NAB cosomegat)`

e = NABωsinωt

e = 2πfNABsinωt

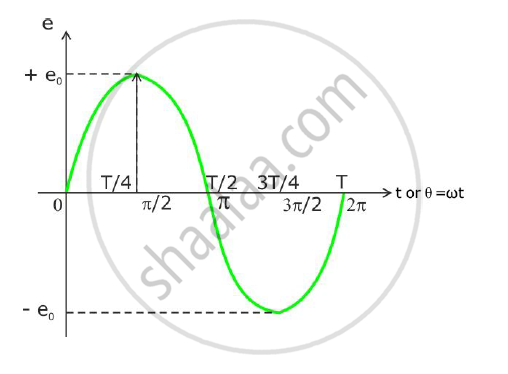
This is the expression for induced e.m.f. generated in the coil at any instant t. It is known as instantaneous e.m.f.

Given that

R/L = σ = 0.1Ω/cm = 0.1 x 100 = 10Ω/m

l₁ = 300 cm = 3 m, E₁ = 1.5 V, E₂ = 1.4 V

We know that

E₁ = iR₁ =iσl₁

`therefore i=E_1/(sigmal_1)=1.5/(10xx3)=0.05 A`

Hence, the current for the other cell is 0.05 A.

For potentiometer, the balancing condition is

`E_1/E_2=l_1/l_2`

`thereforel_2=l_1E_2/E_1=3xx1.4/1.5=2.8m`

So, the balancing length for the other cell is 2.8 m.