Advertisements
Advertisements
प्रश्न
Obtain an expression for electric potential ‘V’ at a point in an end-on position i.e. axial position of the electric dipole.
उत्तर
Electric potential at point P is the sum of electric potential due to the two charges – q and + q of the electric dipole, situated at A and B respectively as shown in the figure.
`therefore V = V_(-q) + V_+q = - k q/((AP)) + k (q)/(BP)`
= `K_q (1/(BP) - 1/(AP)) - K_q (1/(r-a) - 1/(r+a))` 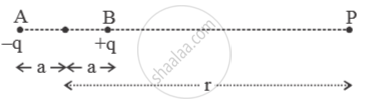
= `k_q {((r+a) - (r-a))/(r^2 - a^2}} = K_q {(2a)/(r^2 - a^2}}`
⇒ `V = k.((q xx 2a))/(r^2 - a^2) = k.P/(r^2 - a^2)` (`p = q xx 2a` is the electric dipole moment)
As a << r (Since dipole has a very small size.)
So `r^2 - a^2 ≈ r^2`
`therefore V ≈ KP/r^2 = 1/(4pi∈_0).P/r^2`
APPEARS IN
संबंधित प्रश्न
Draw a plot showing the variation of (i) electric field (E) and (ii) electric potential (V) with distance r due to a point charge Q.
Can two equi-potential surfaces intersect each other? Give reasons.
Fill in the blank.
The physical quantity having SI unit NC–1m is __________.
Electric Potential V at a point in an electrical field is ______.
Electric potential at a distance r from a point charges q is _________.
The electric potential inside a conducting sphere ______.
Which of the following about potential at a point due to a given point charge is true?
The potential at a point P due to a given point charge ______.
In a certain region of space, the electric field is zero. From this fact, what can you conclude about the electric potential in this region?
Calculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
Calculate potential on the axis of a disc of radius R due to a charge Q uniformly distributed on its surface.
