Advertisements
Advertisements
Question
Obtain an expression for electric potential ‘V’ at a point in an end-on position i.e. axial position of the electric dipole.
Solution
Electric potential at point P is the sum of electric potential due to the two charges – q and + q of the electric dipole, situated at A and B respectively as shown in the figure.
`therefore V = V_(-q) + V_+q = - k q/((AP)) + k (q)/(BP)`
= `K_q (1/(BP) - 1/(AP)) - K_q (1/(r-a) - 1/(r+a))` 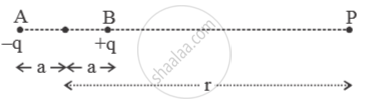
= `k_q {((r+a) - (r-a))/(r^2 - a^2}} = K_q {(2a)/(r^2 - a^2}}`
⇒ `V = k.((q xx 2a))/(r^2 - a^2) = k.P/(r^2 - a^2)` (`p = q xx 2a` is the electric dipole moment)
As a << r (Since dipole has a very small size.)
So `r^2 - a^2 ≈ r^2`
`therefore V ≈ KP/r^2 = 1/(4pi∈_0).P/r^2`
APPEARS IN
RELATED QUESTIONS
Draw a plot showing the variation of (i) electric field (E) and (ii) electric potential (V) with distance r due to a point charge Q.
Can two equi-potential surfaces intersect each other? Give reasons.
Two charges −q and +q are located at points A (0, 0, −a) and B (0, 0, +a) respectively. How much work is done in moving a test charge from point P (7, 0, 0) to Q (−3, 0, 0)?
Electric Potential V at a point in an electrical field is ______.
In a system of n point charges electric potential at a point P having a distance ri from the charge qi is ________.
Which of the following about potential at a point due to a given point charge is true?
The potential at a point P due to a given point charge ______.
In a certain region of space, the electric field is zero. From this fact, what can you conclude about the electric potential in this region?
The electric potential at the surface of an atomic nucleus (Z = 50) of radius 9.0 × 10-15m is
Calculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
Calculate electric potential at a point P which is at a distance of 9 cm from a point charge of 50 μC.
