Advertisements
Advertisements
Question
Calculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
Solution
Let us take point P to be at a distance z from the centre of the ring, as shown in figure. The charge element dq is at a distance z from point P. Therefore, V can be written as
V = `1/(4piε_0) int (dq)/r = 1/(4piε_0) int (dq)/sqrt(z^2 + a^2)`
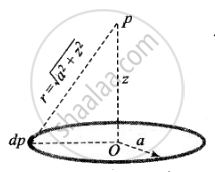
Since each element dq is at the same distance from point P, so we have net potential
V = `1/(4piε_0) 1/sqrt(z^2 + a^2) int dq = 1/(4piε_0) 1/sqrt(z^2 + a^2) [Q]`
The net electric potential V = `1/(4piε_0) Q/sqrt(z^2 + a^2)`
APPEARS IN
RELATED QUESTIONS
Can two equi-potential surfaces intersect each other? Give reasons.
Two charges −q and +q are located at points A (0, 0, −a) and B (0, 0, +a) respectively. How much work is done in moving a test charge from point P (7, 0, 0) to Q (−3, 0, 0)?
A hollow metal sphere and a solid metal sphere of equal radii are given equal charges. Which of the two will have higher potential?
Fill in the blank.
The physical quantity having SI unit NC–1m is __________.
Electric potential is potential energy ______.
In a system of n point charges electric potential at a point P having a distance ri from the charge qi is ________.
The electric potential inside a conducting sphere ______.
In a certain region of space, the electric field is zero. From this fact, what can you conclude about the electric potential in this region?
The electric potential at the surface of an atomic nucleus (Z = 50) of radius 9.0 × 10-15m is
Calculate potential on the axis of a disc of radius R due to a charge Q uniformly distributed on its surface.
