Advertisements
Advertisements
Question
Find the equation of the equipotentials for an infinite cylinder of radius r0, carrying charge of linear density λ.
Solution
To find the potential at distance r from the line consider the electric field. We note that from symmetry the field lines must be radially outward. Draw a cylindrical Gaussian surface of radius r and length l. Then
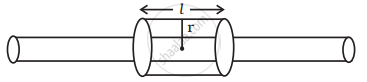
`oint E.dS = 1/ε_0 λ1`
Or `E_r.2pirl = 1/ε_0 λ1`
⇒ `E_r = lambda/(2piε_0r)`
Hence, if r0 is the radius,
`V(r) - V(r_0) = - int_(r_0)^r E.dl = λ/(2piε_0)ln r_0/r`
For a given V,
ln `r/r_0 = - (2piε_0)/λ [V(r) - V(r_0)]`
⇒ r = r0e –2πε0Vr0/λe + 2πε0V(r)/λ
The equipotential surfaces are cylinders of radius r = r0e –2πε0[V(r) – V(r0)]/λ
APPEARS IN
RELATED QUESTIONS
Draw a sketch of equipotential surfaces due to a single charge (-q), depicting the electric field lines due to the charge
A man fixes outside his house one evening a two metre high insulating slab carrying on its top a large aluminium sheet of area 1 m2. Will he get an electric shock if he touches the metal sheet next morning?
Answer the following question.
Two identical point charges, q each, are kept 2m apart in the air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
Depict the equipotential surface due to
(i) an electric dipole,
(ii) two identical positive charges separated by a distance.
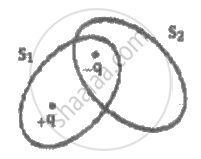
S1 and S2 are the two imaginary surfaces enclosing the charges +q and -q as shown. The electric flux through S1 and S2 are respectively ______.
Equipotentials at a great distance from a collection of charges whose total sum is not zero are approximately.
Can two equipotential surfaces intersect each other?
What is meant by an equipotential surface?
