Advertisements
Advertisements
प्रश्न
Obtain the expression for the period of a magnet vibrating in a uniform magnetic field and performing S.H.M.
उत्तर १
The expression is given as T = `2pi sqrt("I"/"μB")`
Explanation:
The time period of oscillation of a magnet in a uniform magnetic field 'B' is given by
Formula:
T = `2pi sqrt("I"/"μB")`
Where
- T = Time period
- I = Moment of inertia
- μ = magnetic dipole moment
- B = magnetic field
The time period of an oscillating body about a fixed point can be defined as the time taken by the body to complete one vibration around that particular point, called the time period.
उत्तर २
- If a bar magnet is freely suspended in the plane of a uniform magnetic field, it remains in equilibrium with its axis parallel to the direction of the field.
If it is given a small angular displacement θ about an axis passing through its centre, perpendicular to itself and to the field, and released, it performs angular oscillations. - Let μ be the magnetic dipole moment and B the magnetic field. In the deflected position, a restoring torque acts on the magnet that tends to bring it back to its equilibrium position.

Magnet vibrating in a uniform magnetic field - The magnitude of this torque is τ = µBsinθ
If θ is small, sinθ ≈ θ
∴ τ = µBθ - For clockwise angular displacement θ, the restoring torque is in the anticlockwise direction.
∴ τ = Iα = –μBθ
Where I is the moment of inertia of the bar magnet and α is its angular acceleration.
∴ α = `-((mu"B")/"I")θ` ....(1) - Since µ, B, and I are constants, equation (1) shows that angular acceleration is directly proportional to the angular displacement and directed opposite to the angular displacement. Hence the magnet performs angular S.H.M.
- The period of vibrations of the magnet is given by
T = `(2pi)/sqrt("angular acceleration per unit angular displacement")`
= `(2pi)/sqrt(alpha"/"theta)`
Thus, by considering the magnitude of angular acceleration (α),
T = `2pisqrt(("I")/(mu"B"))`
APPEARS IN
संबंधित प्रश्न
Choose the correct option:
A particle performs linear S.H.M. starting from the mean position. Its amplitude is A and time period is T. At the instance when its speed is half the maximum speed, its displacement x is ______.
A particle performing linear S.H.M. of period 2π seconds about the mean position O is observed to have a speed of `"b" sqrt3` m/s, when at a distance b (metre) from O. If the particle is moving away from O at that instant, find the time required by the particle, to travel a further distance b.
The displacement of an oscillating particle is given by x = a sin ω t + b cos ω t where a, b and ω are constants. Prove that the particle performs a linear S.H.M. with amplitude A = `sqrt("a"^2 + "b"^2)`.
A wooden block of mass m is kept on a piston that can perform vertical vibrations of adjustable frequency and amplitude. During vibrations, we don’t want the block to leave the contact with the piston. How much maximum frequency is possible if the amplitude of vibrations is restricted to 25 cm? In this case, how much is the energy per unit mass of the block? (g ≈ π2 ≈ 10 m/s-2)
The period of oscillation of the simple pendulum increases by 20 %, when its length is increased by 44 cm. find its initial length.
What is meant by periodic motion? Give any two examples, for periodic motion.
What is meant by non-periodic motion? Give any two examples, for non-periodic motion.
What is meant by the force constant of a spring?
A particle performs simple harmonic motion with period of 3s. The time taken by It to cover a distance equal to half the amplitude from mean position is [sin 30° = 0.5]
A body of mass 64 g is made to oscillate turn by turn on two different springs A and B. Spring A and B has force constant 4 `"N"/"m"` and `16 "N"/"m"` respectively. If T1 and T2 are period of m oscillations of springs A and B respectively, then `("T"_1 + "T"_2)/("T"_1 - "T"_2)` will be ______.
The ratio of frequencies of oscillations of two simple pendulums is 3: 4 then their lengths are in the ratio ______.
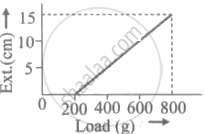
The pointer reading v/s load graph for a spring balance is as given in the figure. The spring constant is ______.
The path length of oscillation of simple pendulum of length 1 meter is 16 cm. Its maximum velocity is ______. (g = π2 m/s2)
If KS and KP respectively are effective spring constants in series and parallel configurations of springs as shown in the figure. Find `K_S/K_P`.
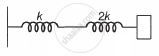 |
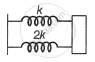 |
| (i) | (ii) |
A block of mass 40 grams is suspended from an ideal spring and set into vertical oscillations. Find the mass to be added on the spring such that the period of oscillation increases by 25%.
Define the term oscillation.
