Advertisements
Advertisements
प्रश्न
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical. Find the surface charge density on the plate.
उत्तर
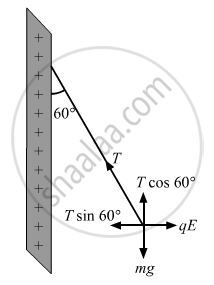
There are two forces acting on the ball. These are
(1) Weight of the ball, W = mg
(2) Coulomb force acting on the charged ball due to the electric field of the plate, F = qE
Due to these forces,a tension develops in the thread.
Let the surface charge density on the plate be σ.
Electric field of a plate,
`"E" = sigma /(2∈_0)`
It is given that in equilibrium, the thread makes an angle of 60° with the vertical.
Resolving the tension in the string along horizontal and vertical directions, we get:
T cos 60° = mg
T sin 60° = qE
`=> tan 60° = "qE"/"mg"`
`=> "E" = ("mg" tan 60 °)/q`
Also, electric field due to a plate,
`"E" = sigma/ 2 ∈_0 =( "mg" tan 60°)/q`
`sigma =(2 ∈_0 "mg" tan 60 °)/"q"`
`sigma =( 2 xx (8.55 xx 10^-12 ) xx ( 10 xx 10 ^-3 xx 9.8) xx 1.7320)/(4.0 xx 10^-6)`
σ = 7.5× 10-7 C/m2
APPEARS IN
संबंधित प्रश्न
Check that the ratio ke2/G memp is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?
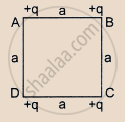
Four charges +q, −q, +q and −q are to be arranged respectively at the four corners of a square ABCD of side 'a'.
(a) Find the work required to put together this arrangement.
(b) A charge q0 is brought to the centre of the square, the four charges being held fixed. How much extra work is needed to do this ?
Find the dimensional formula of ε0.
A charge of 1.0 C is placed at the top of your college building and another equal charge at the top of your house. Take the separation between the two charges to be 2.0 km. Find the force exerted by the charges on each other. How many times your weight is this force?
Estimate the number of electrons in 100 g of water. How much is the total negative charge on these electrons?
Two insulating small spheres are rubbed against each other and placed 1 cm apart. If they attract each other with a force of 0.1 N, how many electrons were transferred from one sphere to the other during rubbing?
Two identical balls, each with a charge of 2.00 × 10−7 C and a mass of 100 g, are suspended from a common point by two insulating strings, each 50 cm long. The balls are held at a separation 5.0 cm apart and then released. Find.
(a) the electric force on one of the charged balls
(b) the components of the resultant force on it along and perpendicular to the string
(c) the tension in the string
(d) the acceleration of one of the balls. Answers are to be obtained only for the instant just after the release.
Two identical pith balls are charged by rubbing one against the other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. In equilibrium, the separation between the balls is 3 cm. Find the mass of each ball and the tension in the strings. The charge on each ball has a magnitude 2.0 × 10−8 C.
A particle with a charge of 2.0 × 10−4 C is placed directly below and at a separation of 10 cm from the bob of a simple pendulum at rest. The mass of the bob is 100 g. What charge should the bob be given so that the string becomes loose?
A water particle of mass 10.0 mg and with a charge of 1.50 × 10−6 C stays suspended in a room. What is the magnitude of electric field in the room? What is its direction ?
Two charged particles, with equal charges of 2.0 × 10−5 C, are brought from infinity to within a separation of 10 cm. Find the increase in the electric potential energy during the process
Two particles of masses 5.0 g each and opposite charges of +4.0 × 10−5 C and −4.0 × 10−5 C are released from rest with a separation of 1.0 m between them. Find the speeds of the particles when the separation is reduced to 50 cm.
Two-point charges of + 0.2 µµC and -0.2 µµC are separated by 1 o8 m. What is the value of the electric field at an axial point at a distance of 0.1 m from their mid-point?
The ratio of the forces between two small spheres with constant charge (a) in air (b) in a medium of dielectric constant K is ______.
Two positive charges ______.
Four equal charges q are placed at the four comers A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be ______.
Two charges of equal magnitudes kept at a distance r exert a force F on each other. If the charges are halved and distance between them is doubled, then the new force acting on each charge is ______.
There is another useful system of units, besides the SI/mks A system, called the cgs (centimeter-gram-second) system. In this system Coloumb’s law is given by
F = `(Qq)/r^2 hatr`
where the distance r is measured in cm (= 10–2 m), F in dynes (= 10–5 N) and the charges in electrostatic units (es units), where 1 es unit of charge = `1/([3]) xx 10^-9 C`
The number [3] actually arises from the speed of light in vaccum which is now taken to be exactly given by c = 2.99792458 × 108 m/s. An approximate value of c then is c = [3] × 108 m/s.
(i) Show that the coloumb law in cgs units yields
1 esu of charge = 1 (dyne)1/2 cm.
Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge = x C, where x is a dimensionless number. Show that this gives
`1/(4pi ∈_0) = 10^-9/x^2 (N*m^2)/C^2`
With `x = 1/([3]) xx 10^-9`, we have `1/(4pi ∈_0) = [3]^2 xx 10^9 (Nm^2)/C^2`
or, `1/(4pi ∈_0) = (2.99792458)^2 xx 10^9 (Nm^2)/C^2` (exactly).
