Advertisements
Advertisements
प्रश्न
One end of a steel rod (K = 46 J s−1 m−1°C−1) of length 1.0 m is kept in ice at 0°C and the other end is kept in boiling water at 100°C. The area of cross section of the rod is 0.04 cm2. Assuming no heat loss to the atmosphere, find the mass of the ice melting per second. Latent heat of fusion of ice = 3.36 × 105 J kg−1.
उत्तर
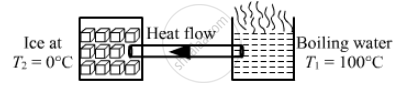
Given:
Thermal conductivity of the rod, K = 46 J s–1 m–1 °C–1
Length of the rod, l = 1 m
Area of the cross-section of the rod, A =0.04 cm2
= 0.04 × 10−4 m2
= 4 × 10−6 m2
Rate of transfer of heat is given by
`(ΔQ)/(Δt) = (ΔT)/ (l/(KA)`
`(ΔQ)/(Δt) = ((T_1 - T_2 ) KA ) / l`
`(ΔQ)/(Δt) =( (100-0 )/1) xx 46 xx 4 xx 10^-6 m^2`
`(DeltaQ)/(Deltat) = 184xx10^-4 J//s`
Also , ΔQ = mL f
`therefore (m/t)L_f = 184 xx 10^-4`
`⇒ ( m/t) xx 3.36 xx 10^5 = 184 xx 10^`
`rArr m=(184xx10^-4)/(3.36xx10^5)xxt`
`rArr m = 5.5xx10^-9xx1 kg//s`
`⇒ m = 5.5 xx 10^-8 xx 10^3 g/s`
`⇒ m = 5.5 xx 10^-5 g/s`
APPEARS IN
संबंधित प्रश्न
Explain why a brass tumbler feels much colder than a wooden tray on a chilly day
A tightly closed metal lid of a glass bottle can be opened more easily if it is put in hot water for some time. Explain.
A metal sheet with a circular hole is heated. The hole
Two identical rectangular strips, one of copper and the other of steel, are riveted together to form a bimetallic strip (acopper> asteel). On heating, this strip will
A glass window is to be fit in an aluminium frame. The temperature on the working day is 40°C and the glass window measures exactly 20 cm × 30 cm. What should be the size of the aluminium frame so that there is no stress on the glass in winter even if the temperature drops to 0°C? Coefficients of linear expansion for glass and aluminium are 9.0 × 10–6 °C–1 and 24 ×100–6°C–1 , respectively.
A steel frame (K = 45 W m−1°C−1) of total length 60 cm and cross sectional area 0.20 cm2, forms three sides of a square. The free ends are maintained at 20°C and 40°C. Find the rate of heat flow through a cross section of the frame.
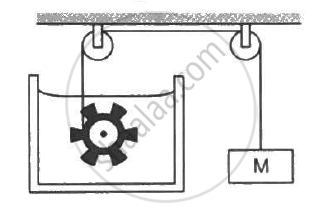
Following Figure shows water in a container having 2.0 mm thick walls made of a material of thermal conductivity 0.50 W m−1°C−1. The container is kept in a melting-ice bath at 0°C. The total surface area in contact with water is 0.05 m2. A wheel is clamped inside the water and is coupled to a block of mass M as shown in the figure. As the block goes down, the wheel rotates. It is found that after some time a steady state is reached in which the block goes down with a constant speed of 10 cm s−1 and the temperature of the water remains constant at 1.0°C. Find the mass M of the block. Assume that the heat flows out of the water only through the walls in contact. Take g = 10 m s−2.
On a winter day when the atmospheric temperature drops to −10°C, ice forms on the surface of a lake. (a) Calculate the rate of increase of thickness of the ice when 10 cm of the ice is already formed. (b) Calculate the total time taken in forming 10 cm of ice. Assume that the temperature of the entire water reaches 0°C before the ice starts forming. Density of water = 1000 kg m−3, latent heat of fusion of ice = 3.36 × 105 J kg−1and thermal conductivity of ice = 1.7 W m−1°C−1. Neglect the expansion of water of freezing.
A semicircular rod is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross section of the semicircular rod to the heat transferred through a cross section of the straight rod in a given time.
Steam at 120°C is continuously passed through a 50 cm long rubber tube of inner and outer radii 1.0 cm and 1.2 cm. The room temperature is 30°C. Calculate the rate of heat flow through the walls of the tube. Thermal conductivity of rubber = 0.15 J s−1 m−1°C−1.
Consider the situation shown in the figure . The frame is made of the same material and has a uniform cross-sectional area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at 100°C is 130 J.

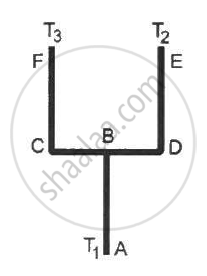
Four identical rods AB, CD, CF and DE are joined as shown in following figure . The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1, T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.
There are two identical vessels filled with equal amounts of ice. The vessels are of different metals. If the ice melts in the two vessels in 20 and 35 minutes respectively, the ratio of the coefficients of thermal conductivity of the two metals is:
These days people use steel utensils with copper bottom. This is supposed to be good for uniform heating of food. Explain this effect using the fact that copper is the better conductor.
We would like to prepare a scale whose length does not change with temperature. It is proposed to prepare a unit scale of this type whose length remains, say 10 cm. We can use a bimetallic strip made of brass and iron each of different length whose length (both components) would change in such a way that difference between their lengths remain constant. If αiron = 1.2 × 10−5/K and αbrass = 1.8 × 10−5/K, what should we take as length of each strip?
A cylinder of radius R made of material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 3R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. What is the effective thermal conductivity of the system?
