Question

OPQ is the sector of a circle having centre at O and radius 15 cm. If m∠POQ = 30°, find the area enclosed by arc PQ and chord PQ.

Answer 1

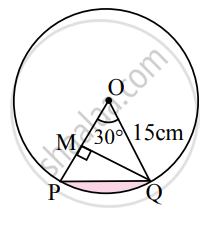
Here, OP = OQ = r = 15 cm

Also, m∠POQ = 30°

= `(30 xx pi/180)^"c"`

= `pi^"c"/6`

∴ θ = `pi^"c"/6`

Now, area of sector OPQ = `1/2"r"^2theta`

= `1/2(15)^2(pi/6)`

= `(225pi)/12"sq cm"`

Let QM be the perpendicular from Q to OP meeting it at M.

Then `l("QM") = 1/2 xx l("OQ") = 15/2"cm"`

∴ area of ΔOPQ = `1/2 xx l("OP") xx l("QM")`

= `1/2 xx 15 xx 15/2`

= `225/4"sq cm"`

Hence, the area between arc PQ and chord PQ

= area of sector OPQ – area of ΔOPQ

= `(225pi)/12 - 225/4`

= `225/4(pi/3 - 1)"sq cm"`.