Advertisements
Advertisements
प्रश्न
People’s monthly electric bills in Chennai are normally distributed with a mean of ₹ 225 and a standard deviation of ₹ 55. Those people spend a lot of time online. In a group of 500 customers, how many would we expect to have a bill that is ₹ 100 or less?
उत्तर
Let X be a normally distributed variable with a mean of ₹ 225 and a standard deviation of ₹ 55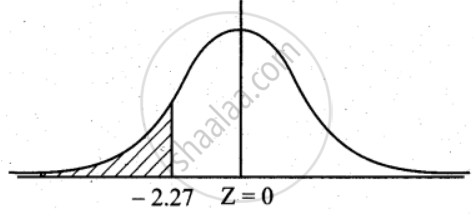
Here µ = 225 and σ = 55
The standard normal variate z = `(x - mu)/sigma = (x - 225)/55`
P(a bill have ₹ 100 or less) = P(X ≤ 100)
When x = 100
z = `(100 - 25)/55`
= `(-125)/55`
= – 2.27
P(X ≤ 100) = P(Z < – 2.27)
P(z < – 2.27) = P(`-oo` < z < 0) – P(– 2.27 < z < 0)
= 0.5 – P(0 < z < 2.27)
= 0.5 – 04884
= 0.0116
APPEARS IN
संबंधित प्रश्न
Mention the properties of binomial distribution.
If 18% of the bolts produced by a machine are defective, determine the probability that out of the 4 bolts chosen at random none will be defective
The average number of phone calls per minute into the switchboard of a company between 10.00 am and 2.30 pm is 2.5. Find the probability that during one particular minute there will be atleast 5 calls
The distribution of the number of road accidents per day in a city is poisson with mean 4. Find the number of days out of 100 days when there will be atleast 2 accidents
X is normally distributed with mean 12 and SD 4. Find P(X ≤ 20) and P(0 ≤ X ≤ 12)
Choose the correct alternative:
Forty percent of the passengers who fly on a certain route do not check in any luggage. The planes on this route seat 15 passengers. For a full flight, what is the mean of the number of passengers who do not check in any luggage?
Choose the correct alternative:
The weights of newborn human babies are normally distributed with a mean of 3.2 kg and a standard deviation of 1.1 kg. What is the probability that a randomly selected newborn baby weight less than 2.0 kg?
The time taken to assemble a car in a certain plant is a random variable having a normal distribution of 20 hours and a standard deviation of 2 hours. What is the probability that a car can be assembled at this plant in a period of time. Less than 19.5 hours?
The time taken to assemble a car in a certain plant is a random variable having a normal distribution of 20 hours and a standard deviation of 2 hours. What is the probability that a car can be assembled at this plant in a period of time. Between 20 and 22 hours?
The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000. What percent of people earn less than $40,000?
