Advertisements
Advertisements
Question
People’s monthly electric bills in Chennai are normally distributed with a mean of ₹ 225 and a standard deviation of ₹ 55. Those people spend a lot of time online. In a group of 500 customers, how many would we expect to have a bill that is ₹ 100 or less?
Solution
Let X be a normally distributed variable with a mean of ₹ 225 and a standard deviation of ₹ 55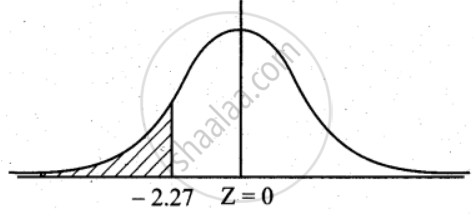
Here µ = 225 and σ = 55
The standard normal variate z = `(x - mu)/sigma = (x - 225)/55`
P(a bill have ₹ 100 or less) = P(X ≤ 100)
When x = 100
z = `(100 - 25)/55`
= `(-125)/55`
= – 2.27
P(X ≤ 100) = P(Z < – 2.27)
P(z < – 2.27) = P(`-oo` < z < 0) – P(– 2.27 < z < 0)
= 0.5 – P(0 < z < 2.27)
= 0.5 – 04884
= 0.0116
APPEARS IN
RELATED QUESTIONS
If 5% of the items produced turn out to be defective, then find out the probability that out of 20 items selected at random there are find the mean and variance
Assume that a drug causes a serious side effect at a rate of three patients per one hundred. What is the probability that atleast one person will have side effects in a random sample of ten patients taking the drug?
Consider five mice from the same litter, all suffering from Vitamin A deficiency. They are fed a certain dose of carrots. The positive reaction means recovery from the disease. Assume that the probability of recovery is 0.73. What is the probability that atleast 3 of the 5 mice recover
The average number of phone calls per minute into the switchboard of a company between 10.00 am and 2.30 pm is 2.5. Find the probability that during one particular minute there will be exactly 3 calls
The average number of customers, who appear in a counter of a certain bank per minute is two. Find the probability that during a given minute no customer appears
If the heights of 500 students are normally distributed with mean 68.0 inches and standard deviation 3.0 inches, how many students have height between 65 and 71 inches
Time taken by a construction company to construct a flyover is a normal variate with mean 400 labour days and a standard deviation of 100 labour days. If the company promises to construct the flyover in 450 days or less and agree to pay a penalty of ₹ 10,000 for each labour day spent in excess of 450. What is the probability that the company pay a penalty of at least ₹ 2,00,000?
Choose the correct alternative:
The random variable X is normally distributed with a mean of 70 and a standard deviation of 10. What is the probability that X is between 72 and 84?
Choose the correct alternative:
Cape town is estimated to have 21% of homes whose owners subscribe to the satellite service, DSTV. If a random sample of your home is taken, what is the probability that all four homes subscribe to DSTV?
X is a normally distributed variable with mean µ = 30 and standard deviation σ = 4. Find P(X > 21)
