Advertisements
Advertisements
Question
X is a normally distributed variable with mean µ = 30 and standard deviation σ = 4. Find P(X > 21)
Solution
Given X ~ N(µ, σ2)
µ = 30
σ = 4
P(X > 21) = `"P"("Z" > (21 - 30)/4)`
= P(Z > – 2.25)
= 0.5 + P(– 2.25 < Z < 0)
= 0 5 + P(0 < Z < 2.25)
= 0.5 + 0.4878
= 0.9878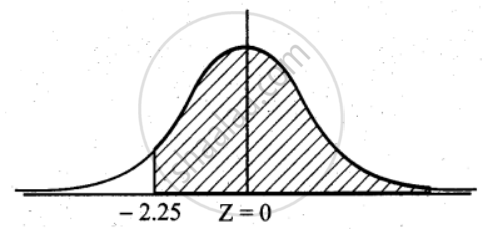
APPEARS IN
RELATED QUESTIONS
If 18% of the bolts produced by a machine are defective, determine the probability that out of the 4 bolts chosen at random exactly one will be defective
The mortality rate for a certain disease is 7 in 1000. What is the probability for just 2 deaths on account of this disease in a group of 400? [Given e–2.8 = 0.06]
A car hiring firm has two cars. The demand for cars on each day is distributed as a Poison variate, with mean 1.5. Calculate the proportion of days on which neither car is used
The average number of phone calls per minute into the switchboard of a company between 10.00 am and 2.30 pm is 2.5. Find the probability that during one particular minute there will be no phone at all
Define Normal distribution
If the heights of 500 students are normally distributed with mean 68.0 inches and standard deviation 3.0 inches, how many students have height greater than 72 inches
Time taken by a construction company to construct a flyover is a normal variate with mean 400 labour days and a standard deviation of 100 labour days. If the company promises to construct the flyover in 450 days or less and agree to pay a penalty of ₹ 10,000 for each labour day spent in excess of 450. What is the probability that the company takes at most 500 days to complete the flyover?
Choose the correct alternative:
The average percentage of failure in a certain examination is 40. The probability that out of a group of 6 candidates atleast 4 passed in the examination are
Choose the correct alternative:
Cape town is estimated to have 21% of homes whose owners subscribe to the satellite service, DSTV. If a random sample of your home is taken, what is the probability that all four homes subscribe to DSTV?
The birth weight of babies is Normally distributed with mean 3,500g and standard deviation 500g. What is the probability that a baby is born that weighs less than 3,100g?
