Advertisements
Advertisements
Question
X is a normally distributed variable with mean µ = 30 and standard deviation σ = 4. Find P(X < 40)
Solution
Given X ~ N(µ, σ2)
µ = 30
σ = 4
P(X < 40) = `"P"("Z" < (40 -30)/4)`
= P(Z < 2.5)
= 0.5 + P(0 < Z < 2.5)
= 0.5 + 0.4938
= 0.9938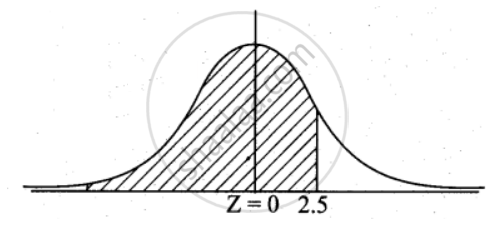
APPEARS IN
RELATED QUESTIONS
If 5% of the items produced turn out to be defective, then find out the probability that out of 20 items selected at random there are atleast two defectives
Among 28 professors of a certain department, 18 drive foreign cars and 10 drive local made cars. If 5 of these professors are selected at random, what is the probability that atleast 3 of them drive foreign cars?
The average number of customers, who appear in a counter of a certain bank per minute is two. Find the probability that during a given minute no customer appears
Write down any five chief characteristics of Normal probability curve
If the heights of 500 students are normally distributed with mean 68.0 inches and standard deviation 3.0 inches, how many students have height between 65 and 71 inches
In a photographic process, the developing time of prints may be looked upon as a random variable having the normal distribution with a mean of 16.28 seconds and a standard deviation of 0.12 second. Find the probability that it will take less than 16.35 seconds to develop prints
Vehicles pass through a junction on a busy road at an average rate of 300 per hour. Find the probability that none passes in a given minute
Vehicles pass through a junction on a busy road at an average rate of 300 per hour. What is the expected number passing in two minutes?
The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000. What percent of people earn less than $40,000?
The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000. What percent of people earn more than $75,000
