Advertisements
Advertisements
Question
The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000. What percent of people earn more than $75,000
Solution
Let x denotes the annual salaries of employees in a large company
Mean µ = 50,000 and S.D σ = 20,000
Standard normal variate z = `(x - mu)/sigma`
P(people earn more than$75,000) = P(X > 70000)
When x = 75,000
z = `(75,000 - 50, 000)/(20,000)`
= `25000/20000`
= `5/4`
z = 1.25
P(X > 75,000) = P(X > 1.25)
= P(0 < z < `oo`) – P(0 < z < 1.25)
= 0.5 – 0.3944
= 0.1056
P(x > 750,000) in percent
= 01056 × 100
= 10.56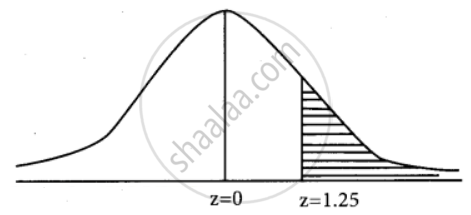
APPEARS IN
RELATED QUESTIONS
Define Binomial distribution
Write down the condition for which the binomial distribution can be used.
Defects in yarn manufactured by a local mill can be approximated by a distribution with a mean of 1.2 defects for every 6 metres of length. If lengths of 6 metres are to be inspected, find the probability of less than 2 defects
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of 2 successes
The mean of a binomial distribution is 5 and standard deviation is 2. Determine the distribution
Derive the mean and variance of poisson distribution
The average number of customers, who appear in a counter of a certain bank per minute is two. Find the probability that during a given minute no customer appears
Write down the conditions in which the Normal distribution is a limiting case of binomial distribution
Choose the correct alternative:
Cape town is estimated to have 21% of homes whose owners subscribe to the satellite service, DSTV. If a random sample of your home is taken, what is the probability that all four homes subscribe to DSTV?
X is a normally distributed variable with mean µ = 30 and standard deviation σ = 4. Find P(X > 21)
