Advertisements
Advertisements
Question
The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000. What percent of people earn between $45,000 and $65,000?
Solution
Let x denotes the annual salaries of employees in a large company
Mean µ = 50,000 and S.D σ = 20,000
Standard normal variate z = `(x - mu)/sigma`
P(people ear between $45,000 and $65,000)
P(45000 < x < 65000)
When x = 45,000
z = `(45, 000 - 50, 000)/(20, 000)`
= `(-5000)/(20, 000)`
= `(-1)/4`
z = – 0.25
When x = 65,000
z = `(5, 000 - 50, 000)/(20,000)`
= `(15000)/(20, 000)`
= `3/4`
z = 0.75
P(45000 < x < 65000) = P(– 0.25 < z < 0.75)
= P(– 0.25 < z < 0) + P(0 < z < 0.75)
= p(0 < z < 0.25) + P(0 < z < 0.75)
= P(0 < z < 0.25) + P(0 < z < 0.75)
= 0.0987 + 0.2734
= 0.3721
P(45000 < x < 65000) in percentage
= 0.3721 × 100
= 37.21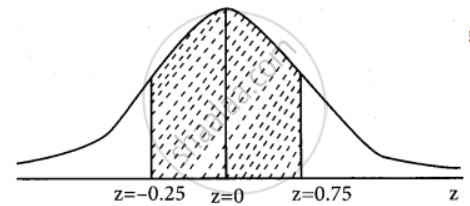
APPEARS IN
RELATED QUESTIONS
Define Binomial distribution
If 18% of the bolts produced by a machine are defective, determine the probability that out of the 4 bolts chosen at random none will be defective
Forty percent of business travellers carry a laptop. In a sample of 15 business travelers, what is the probability that 12 of the travelers will not have a laptop?
Derive the mean and variance of poisson distribution
The average number of phone calls per minute into the switchboard of a company between 10.00 am and 2.30 pm is 2.5. Find the probability that during one particular minute there will be exactly 3 calls
In a test on 2,000 electric bulbs, it was found that bulbs of a particular make, was normally distributed with an average life of 2,040 hours and standard deviation of 60 hours. Estimate the number of bulbs likely to burn for less than 1,950 hours
If the heights of 500 students are normally distributed with mean 68.0 inches and standard deviation 3.0 inches, how many students have height less than or equal to 64 inches
Choose the correct alternative:
If X ~ N(9, 81) the standard normal variate Z will be
Choose the correct alternative:
Cape town is estimated to have 21% of homes whose owners subscribe to the satellite service, DSTV. If a random sample of your home is taken, what is the probability that all four homes subscribe to DSTV?
Choose the correct alternative:
Let z be a standard normal variable. If the area to the right of z is 0.8413, then the value of z must be:
