Question

In a test on 2,000 electric bulbs, it was found that bulbs of a particular make, was normally distributed with an average life of 2,040 hours and standard deviation of 60 hours. Estimate the number of bulbs likely to burn for less than 1,950 hours

Answer 1

Let x denote the burning of the bulb follows normal distribution with mean 2,040 and standard deviation 60 hours.

Here m = 2040

σ = 60 

N = 2000

The standard normal variate

z = `(x - mu)/sigma`

= `(x - 2040)/60`

P(less than 1950 hours)

P(X < 1950)

When x = 1950

z = `(1950 - 3040)/60`

= `(-90)/60`

= – 1.5

P(X < 1950) = P(Z <  – 1.5) = P(Z > 1.5)

= 0.5 – 0.4332

= 0.068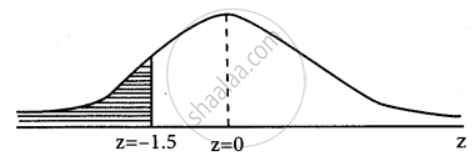

Numbers of bulbs whose burning time is less than
1950

= 0.0668 × 2000

= 133.6

= 134   ......(approximately)