Advertisements
Advertisements
Question
The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000. What percent of people earn less than $40,000?
Solution
Let x denotes the annual salaries of employees in a large company
Mean µ = 50,000 and S.D σ = 20,000
P(people earn less than $40,000) = P(X < 40,000)
When x = 40,000
z = `(40, 000 - 50, 000)/(20 000)`
= `(10,000)/(20,000)`
z = – 0.5
P(X < 40,000) = P(Z < – 0.5)
= P(`-oo` < z < 0) – P(– 0.5 < z < 0)
= 0.5 – P(– 0.5 < z <0)
= 0.5 – P(0 < z < 0.5) ......(Due to symmetry)
= 0.5 – 0.01915
= 0.3085
= P(X < 40,000) in percentage
= 0.3085 × 100
= 30.85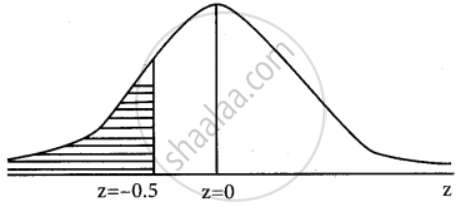
APPEARS IN
RELATED QUESTIONS
If 18% of the bolts produced by a machine are defective, determine the probability that out of the 4 bolts chosen at random exactly one will be defective
Among 28 professors of a certain department, 18 drive foreign cars and 10 drive local made cars. If 5 of these professors are selected at random, what is the probability that atleast 3 of them drive foreign cars?
Out of 750 families with 4 children each, how many families would be expected to have children of both sexes? Assume equal probabilities for boys and girls.
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of 2 successes
Determine the binomial distribution for which the mean is 4 and variance 3. Also find P(X=15)
Write the conditions for which the poisson distribution is a limiting case of binomial distribution
The average number of phone calls per minute into the switchboard of a company between 10.00 am and 2.30 pm is 2.5. Find the probability that during one particular minute there will be exactly 3 calls
Write down any five chief characteristics of Normal probability curve
Choose the correct alternative:
The parameters of the normal distribution f(x) = `(1/sqrt(72pi))"e"^(-(x - 10)^2)/72 - oo < x < oo`
Choose the correct alternative:
An experiment succeeds twice as often as it fails. The chance that in the next six trials, there shall be at least four successes is
