Advertisements
Advertisements
Question
The time taken to assemble a car in a certain plant is a random variable having a normal distribution of 20 hours and a standard deviation of 2 hours. What is the probability that a car can be assembled at this plant in a period of time. Between 20 and 22 hours?
Solution
Let x denotes the time taken to assemable cars mean µ = 20 hours and S.D σ = 2 hours
The standard normal variate
z = `(x - mu)/sigma`
= `(x - 20)/2`
P(Between 20 and 22 hours) = P(20 < x < 22)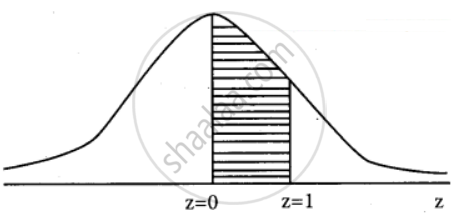
When x = 20
z = `(20 - 20)/2 = 0/2` = 0
When x = 22
z = `(22 - 20)/2 = 2/2` = 1
P(20 < x < 22) = P(0 < z < 1)
= 0.3413
APPEARS IN
RELATED QUESTIONS
Define Poisson distribution
Derive the mean and variance of poisson distribution
The mortality rate for a certain disease is 7 in 1000. What is the probability for just 2 deaths on account of this disease in a group of 400? [Given e–2.8 = 0.06]
A car hiring firm has two cars. The demand for cars on each day is distributed as a Poison variate, with mean 1.5. Calculate the proportion of days on which some demand is refused
If the heights of 500 students are normally distributed with mean 68.0 inches and standard deviation 3.0 inches, how many students have height less than or equal to 64 inches
Choose the correct alternative:
If P(Z > z) = 0.8508 what is the value of z (z has a standard normal distribution)?
A manufacturer of metal pistons finds that on the average, 12% of his pistons are rejected because they are either oversize or undersize. What is the probability that a batch of 10 pistons will contain at least 2 rejects?
Entry to a certain University is determined by a national test. The scores on this test are normally distributed with a mean of 500 and a standard deviation of 100. Raghul wants to be admitted to this university and he knows that he must score better than at least 70% of the students who took the test. Raghul takes the test and scores 585. Will he be admitted to this university?
X is a normally distributed variable with mean µ = 30 and standard deviation σ = 4. Find P(X < 40)
X is a normally distributed variable with mean µ = 30 and standard deviation σ = 4. Find P(30 < X < 35)
