Advertisements
Advertisements
Question
If the heights of 500 students are normally distributed with mean 68.0 inches and standard deviation 3.0 inches, how many students have height less than or equal to 64 inches
Solution
Let x denote the height of a student N = 500; m = 68.0 inches and σ = 3.0 inches the standard normal variate
z = `(x - mu)/sigma = (x - 68)/3`
P(Less than or equal to 64 inches)
P(X ≤ 64)
When x = 64
z = `(64 - 68)/3 = (-4)/3 = - 1.33`
P(X ≤ 64) = P(Z ≤ – 1.33)
P(Z ≥ – 1.33)
= 0.5 – 0.4082
= 0.0918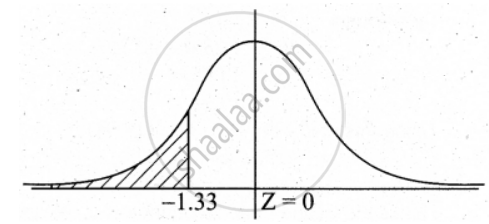
∴ Number of heights who ate less than or equal to 64 inches
= 0.0918 × 500
= 45.9
= 46 .......(approximately)
APPEARS IN
RELATED QUESTIONS
Define Bernoulli trials
If 18% of the bolts produced by a machine are defective, determine the probability that out of the 4 bolts chosen at random exactly one will be defective
Forty percent of business travellers carry a laptop. In a sample of 15 business travelers, what is the probability that 12 of the travelers will not have a laptop?
Define Poisson distribution
Write the conditions for which the poisson distribution is a limiting case of binomial distribution
X is normally distributed with mean 12 and SD 4. Find P(X ≤ 20) and P(0 ≤ X ≤ 12)
Choose the correct alternative:
In a parametric distribution the mean is equal to variance is
Choose the correct alternative:
A manufacturer produces switches and experiences that 2 percent switches are defective. The probability that in a box of 50 switches, there are atmost two defective is :
Choose the correct alternative:
The weights of newborn human babies are normally distributed with a mean of 3.2 kg and a standard deviation of 1.1 kg. What is the probability that a randomly selected newborn baby weight less than 2.0 kg?
Entry to a certain University is determined by a national test. The scores on this test are normally distributed with a mean of 500 and a standard deviation of 100. Raghul wants to be admitted to this university and he knows that he must score better than at least 70% of the students who took the test. Raghul takes the test and scores 585. Will he be admitted to this university?
