Advertisements
Advertisements
Question
X is normally distributed with mean 12 and SD 4. Find P(X ≤ 20) and P(0 ≤ X ≤ 12)
Solution
X is normally distribution with mean 12 and SD 4
∴ µ = 12 and σ = 4
Standard normal variable
z = `(x - mu)/sigma`
= `(x - 12)/4`
P(X ≤ 20)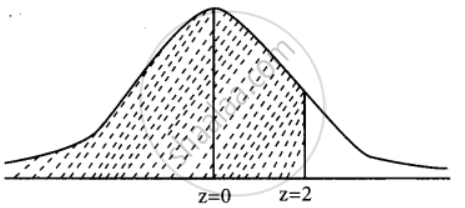
When x = 20
z = `(20 - 12)/4 = 8/4` = 2
v(x ≤ 20) = `8/4` = 2
P(x ≤ 20) = P(z ≤ 2)
= 0.5 + p(0 < z < 2)
= 0.5 + 0.4772
= 0.9772
P(0 ≤ X ≤ 12)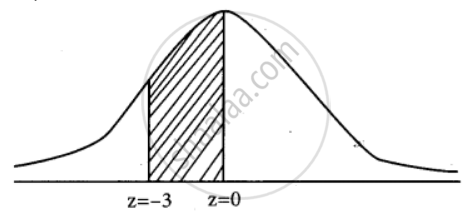
When x = 0
z = `(0 - 12)/4 = (-12)/4 = - 3`
When x = 12
z = `(12 - 12)/4 = 0/4` = 0
P(0 ≤ x ≤ 12) = P(-3 ≤ z ≤ 0)
= P(0 ≤ z ≤ 3)
= 0.4987
APPEARS IN
RELATED QUESTIONS
If 5% of the items produced turn out to be defective, then find out the probability that out of 20 items selected at random there are atleast two defectives
If 18% of the bolts produced by a machine are defective, determine the probability that out of the 4 bolts chosen at random exactly one will be defective
The mortality rate for a certain disease is 7 in 1000. What is the probability for just 2 deaths on account of this disease in a group of 400? [Given e–2.8 = 0.06]
Define Normal distribution
Choose the correct alternative:
The random variable X is normally distributed with a mean of 70 and a standard deviation of 10. What is the probability that X is between 72 and 84?
Choose the correct alternative:
In a large statistics class, the heights of the students are normally distributed with a mean of 172 cm and a variance of 25 cm. What proportion of students is between 165cm and 181 cm in height?
Choose the correct alternative:
In a binomial distribution, the probability of success is twice as that of failure. Then out of 4 trials, the probability of no success is
Hospital records show that of patients suffering from a certain disease 75% die of it. What is the probability that of 6 randomly selected patients, 4 will recover?
The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000. What percent of people earn between $45,000 and $65,000?
The birth weight of babies is Normally distributed with mean 3,500g and standard deviation 500g. What is the probability that a baby is born that weighs less than 3,100g?
