Advertisements
Advertisements
प्रश्न
Places A and B are 160 km apart on a highway. A car starts from A and another car starts from B simultaneously. If they travel in the same direction, they meet in 8 hours. But, if they travel towards each other, they meet in 2 hours. Find the speed of each car.
उत्तर
Let the speed of the car A and B be x km/h and y km/h respectively. Let x > y.
Case-1: When they travel in the same direction

From the figure
AC – BC = 160
⇒ x × 8 – y × 8 = 160
⇒ x – y = 20
Case-2: When they travel in opposite direction
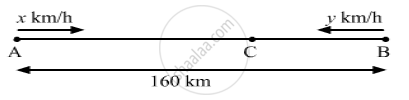
From the figure
AC + BC = 160
⇒ x × 2 + y × 2 = 160
⇒ x + y = 80
Adding (i) and (ii), we get
2x = 100 ⇒ x = 50 km/h
Putting x = 50 in (ii), we have
50 + y = 80 ⇒ y = 80 – 50 = 30 km/h
Hence, the speeds of the cars are 50 km/h and 30 km/h.
APPEARS IN
संबंधित प्रश्न
Obtain the condition for the following system of linear equations to have a unique solution
ax + by = c
lx + my = n
Solve for x and y:
`x + 6/y = 6, 3x - 8/y = 5`
Solve for x and y:
px + qy = p – q,
qx – py = p + q
Solve for x and y:
`(bx)/a - (ay)/b + a + b = 0, bx – ay + 2ab = 0`
Solve for x and y:
`x + y = a + b, ax - by = a^2 - b^2`
Find the value of k for which the system of linear equations has an infinite number of solutions:
kx + 3y = (2k + 1),
2(k + 1)x + 9y = (7k + 1).
Find the value of k for which the system of linear equations has an infinite number of solutions:
(k – 1)x – y = 5,
(k + 1)x + (1 – k)y = (3k + 1).
The sum of two numbers is 137 and their differences are 43. Find the numbers.
If three times the larger of two numbers is divided by the smaller, we get 4 as the quotient and 8 as the remainder. If five times the smaller is divided by the larger, we get 3 as the quotient and 5 as the remainder. Find the numbers.
If 217x + 131y = 913, 131x + 217y = 827, then x + y is ______.
