Advertisements
Advertisements
प्रश्न
ΔPQR मध्ये, ∠P = 40°, PQ ≅ PR, QR = 7 सेमी. ΔXYZ ∼ ΔPQR, XY:PQ = 3:2 असल्यास ΔXYZ काढा.
उत्तर
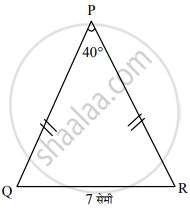
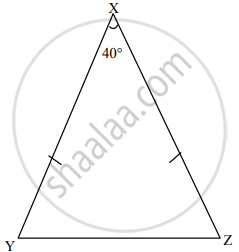
कच्ची आकृती
ΔPQR मध्ये, ∠P = 40°, PQ ≅ PR
∴ ΔPQR हा समद्विभुज त्रिकोण आहे.
∴ ∠Q ≅ ∠R
समजा, ∠Q = ∠R = a
∴ a + a + 40° = 180° ..........[त्रिकोणाच्या सर्व कोनांच्या मापांची बेरीज 180° असते.]
∴ 2a = 140°
∴ a = `140/2`
∴ a = 70°
∴ ∠Q = ∠R = 70°
ΔXYZ ∼ ΔPQR, `"XY"/"PQ" = "YZ"/"QR" = "XZ"/"PR"` .........[समरूप त्रिकोणांच्या संगत बाजू]
∴ `3/2 = "YZ"/7` .....[XY : PQ = 3:2 व QR = 7 सेमी]
∴ YZ = `(7 xx 3)/2 = 10.5` सेमी
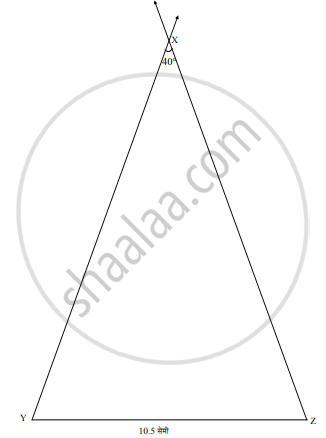
रचनेच्या पायऱ्या:
| क्र. | ΔXYZ |
| i. | रेख YZ = 10.5 सेमी काढा. |
| ii. | बिंदू Y व Z वर 70° अंशाचा कोन करणारे किरण काढा. |
| iii. | त्यांच्या छेदनबिंदूला X नाव द्या. |
APPEARS IN
संबंधित प्रश्न
ΔPQR ~ ΔLTR, ΔPQR मध्ये PQ = 4.2 सेमी, QR = 5.4 सेमी, PR = 4.8 सेमी आणि `"PQ"/"LT"` = `3/4` तर ΔPQR व ΔLTR काढा.
ΔRST ~ ΔXYZ, ΔRST मध्ये RS = 4.5 सेमी, ∠RST = 40°, ST = 5.7 सेमी आणि `"RS"/"XY" = 3/5` तर ΔRST व ΔXYZ काढा.
ΔAMT ~ ΔAHE, ΔAMT मध्ये AM = 6.3 सेमी, ∠TAM = 50°, AT = 5.6 सेमी आणि `"AM"/"AH" = 7/5` तर ΔAHE काढा.
ΔABC हा 60° काढा व तो दुभागा.
∠PQR हा 115° काढा. त्याचे दोन एकरूप कोनांत विभाजन करा.
ΔABC ∼ ΔPBQ, ΔABC मध्ये , AB = 3 सेमी, ∠B = 90°, BC = 4 सेमी व त्रिकोणाच्या संगत बाजूंचे गुणोत्तर 7:4 असल्यास ΔPBQ काढा.
ΔPQR ∼ ΔABC, ΔPQR मध्ये PQ = 3.6 सेमी, QR = 4 सेमी, PR = 4.2 सेमी आहे. त्रिकोणाच्या संगत बाजूचे गुणोत्तर 3:2 असल्यास ΔABC काढा.
ΔABC ∼ ΔPBQ, ΔABC मध्ये, AB = 4 सेमी, BC = 5 सेमी, AC = 6 सेमी. त्रिकोणाच्या संगत बाजूंचे गुणोत्तर 2:3 असल्यास ΔPBQ काढा.
ΔSHR ∼ ΔSVU, ΔSHR मध्ये SH = 4.5 सेमी, HR = 5.2 सेमी, SR = 5.8 सेमी, `"HS"/"SV" = 3/5`, तर ΔSVU काढा.
ΔPQR ∼ ΔAQB, ΔPQR मध्ये, PQ = 3 सेमी, ∠Q = 90°, QR = 4 सेमी. त्रिकोणाच्या संगत बाजूंचे गुणोत्तर 7:5 असल्यास ΔAQB काढा.
