Advertisements
Advertisements
प्रश्न
ΔPQR ∼ ΔABC, ΔPQR मध्ये PQ = 3.6 सेमी, QR = 4 सेमी, PR = 4.2 सेमी आहे. त्रिकोणाच्या संगत बाजूचे गुणोत्तर 3:2 असल्यास ΔABC काढा.
उत्तर
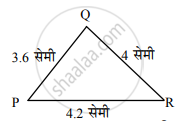
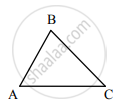
कच्ची आकृती
विश्लेषण:
ΔPQR ∼ ΔABC .............[पक्ष]
∴ `"PQ"/"AB" = "QR"/"BC" = "PR"/"AC"` .......[समरूप त्रिकोणांच्या संगत बाजू]
∴ `"PQ"/"AB" = "QR"/"BC" = "PR"/"AC" = 3/2` ..........[पक्ष]
∴ `3.6/"AB" = 4/"BC" = 4.2/"AC" = 3/2`
∴ `3.6/"AB" = 3/2`
∴ AB = `(3.6 xx 2)/3`
∴ AB = 2.4 सेमी
तसेच, `4/"BC" = 3/2`
∴ BC = `(4 xx 2)/2`
∴ BC = 2.7 सेमी
∴ व `4.2/"AC" = 3/2`
∴ AC = `(4.2 xx 2)/3`
∴ AC = 2.8 सेमी
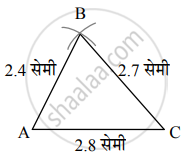
रचनेच्या पायऱ्या:
| क्र. | ΔABC साठी |
| i. | 2.8 सेमी लांबीची रेख AC काढा. |
| ii. | बिंदू A वरून 2.4 सेमी लांबीचा कंस काढा. |
| iii. | बिंदू C वरून 2.7 सेमी लांबीचा कंस काढा. |
| iv. | रेख AB आणि रेख CB जोडा. |
ΔABC हा ΔPQR शी समरूप असणारा इष्ट त्रिकोण आहे.
APPEARS IN
संबंधित प्रश्न
ΔPQR ~ ΔLTR, ΔPQR मध्ये PQ = 4.2 सेमी, QR = 5.4 सेमी, PR = 4.8 सेमी आणि `"PQ"/"LT"` = `3/4` तर ΔPQR व ΔLTR काढा.
ΔPYQ असा काढा की, PY = 6.3 सेमी, YQ = 7.2 सेमी, PQ = 5.8 सेमी. ΔXYZ हा ΔPYQ शी समरूप त्रिकोण असा काढा की, `"YZ"/"YQ" = 6/5`.
रेख AB = 9.7 सेमी लांबीचा काढा. त्यावर बिंदू P असा घ्या, की AP = 3.5 सेमी, A – P – B. बिंदू P मधून रेख AB ला लंब काढा.
ΔABC ∼ ΔPBQ, ΔABC मध्ये, AB = 4 सेमी, BC = 5 सेमी, AC = 6 सेमी. त्रिकोणाच्या संगत बाजूंचे गुणोत्तर 2:3 असल्यास ΔPBQ काढा.
ΔRHP ∼ ΔNED, ΔNED मध्ये, NE = 7 सेमी, ∠D = 30°, ∠N = 20° तसेच `"HP"/"ED" = 4/5,` तर ΔRHP काढा.
ΔABC ~ ΔPBR, BC = 8 सेमी, AC = 10 सेमी , ∠B = 90°, `"BC"/"BR" = 5/4`, तर ΔPBR काढा.
ΔAMT ~ ΔAHE, ΔAMT मध्ये, AM = 6.3 सेमी, ∠TAM = 50°, AT = 5.6 सेमी, `"AM"/"AH" = 7/5`, तर ΔAHE काढा.
ΔSHR ∼ ΔSVU, ΔSHR मध्ये SH = 4.5 सेमी, HR = 5.2 सेमी, SR = 5.8 सेमी, `"HS"/"SV" = 3/5`, तर ΔSVU काढा.
ΔPQR मध्ये, ∠P = 40°, PQ ≅ PR, QR = 7 सेमी. ΔXYZ ∼ ΔPQR, XY:PQ = 3:2 असल्यास ΔXYZ काढा.
चौरसाचा कर्ण `sqrt50` सेमी असून असे वर्तुळ काढा, की जे चौरसाच्या सर्व बाजूंना स्पर्श करेल. वर्तुळाची त्रिज्या मोजून लिहा.
