Advertisements
Advertisements
प्रश्न
परीक्षित प्लास्टिसिन का एक घनाभ बनाता है, जिसकी भुजाएँ 5cm, 2cm और 5cm हैं। एक घन बनाने के लिए ऐसे कितने घनाभों की आवश्यकता होगी?
उत्तर
दिया गया भुजाएँ 5cm, 2cm और 5cm
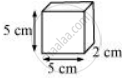
जब इन घनाभों को एक घन बनाने के लिए व्यवस्थित किया जाता है, तो इस प्रकार बने घन की भुजाएँ दिए गए घनाभ की भुजाओं (अर्थात, 5, 2, और 5) का एक सामान्य गुणज होंगी।
इससे एक घनाभ का आयतन = 5 × 2 × 5
10 सेमी भुजा वाला एक घन बनाने का प्रयास करें।
यहाँ आयतन को 2 × 2 × 5 = 20 से गुणा करने पर पूर्ण घन प्राप्त हो जाएगा।
ऐसे मापों के 20 घनाभों की सहायता से एक घन इस प्रकार बनता है:
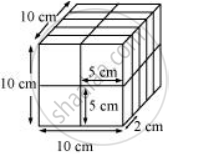
वैकल्पिक
किनारों पर घन का आयतन: 5cm, 2cm, 5cm
= 5 cm× 2 cm× 5 cm = (5 × 5 × 2) cm3
यदि हम इस व्यंजक को 2 × 2 × 5 = 20 से गुणा करें तो यह एक पूर्ण घन बन जाएगा।
इस प्रकार, (5 × 5 × 2 × 2 × 2 × 5) = (5 × 5 × 5 × 2 × 2 × 2) = 1000 एक पूर्ण घन है।
अतः एक घन बनाने के लिए 5cm, 2cm और 5cm के 20 घनाभों की आवश्यकता होती है।
APPEARS IN
संबंधित प्रश्न
वह सबसे छोटी संख्या ज्ञात कीजिए जिससे निम्नलिखित संख्या को भाग देने पर भागफल एक पूर्ण घन प्राप्त हो जाए:
128
वह सबसे छोटी संख्या ज्ञात कीजिए जिससे निम्नलिखित संख्या को भाग देने पर भागफल एक पूर्ण घन प्राप्त हो जाए:
704
यदि किसी संख्या का वर्ग 5 पर समाप्त होता है, तो उसका घन 25 पर समाप्त होता है।
संख्या x के घनमूल को ______ से निरूपित किया जाता है।
8000 का घनमूल 200 है।
यदि a2 अंक 5 पर समाप्त होता है, तो a3, 25 पर समाप्त होगा।
यदि a2 अंक 9 पर समाप्त होता है, तो a3, 7 पर समाप्त होगा।
`root(3)(8 + 27) = root(3)(8) + root(3)(27)` है।
मान निकालिए –
`root(3)(27) + root(3)(0.008) + root(3)(0.064)`
