Advertisements
Advertisements
प्रश्न
Prove that the diagonals of a square are equal and perpendicular to each other.
उत्तर

Given:
ABCD is a square with diagonals AC and BD intersecting each other at point O.
To prove: AC = BD and ∠AOB = 90°
Proof:
In ΔDAB and ΔCBA,
AD = BC ...(Sides of a square)
∠DAB = ∠CBA ...(Each 90)
AB = AB ...(Common)
⇒ ΔDAB ≅ ΔCBA ...(SAS Congruence)
⇒ AC = BD ...(C.P.C.T)
In ΔAOB and ΔBOC,
AD = BC ...(Sides of a square)
OB = OB ...(Common)
OA = OC ...(Diagonals of a square bisect each other)
⇒ ΔAOB ≅ ΔBOC ...(SSS Congruence)
⇒ ∠AOB =∠BOC ...(C.P.C.T)
But, ∠AOB + ∠BOC = 180° ...(Linear pair)
⇒ ∠AOB = ∠BOC = `(180°)/(2)` = 90°
∴ AC = BD ⇒ Diagonals are equal
And, ∠AOB = 90° ⇒ Diagonals are perpendicular to each other.
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram. P and Q are mid-points of AB and CD. Prove that APCQ is also a parallelogram.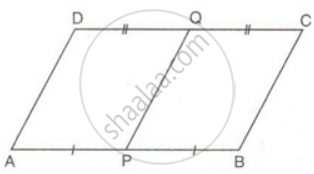
ABCD is a parallelogram. P and T are points on AB and DC respectively and AP = CT. Prove that PT and BD bisect each other.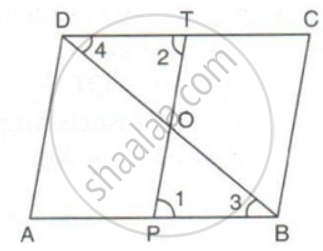
PQRS is a parallelogram. PQ is produced to T so that PQ = QT. Prove that PQ = QT. Prove that ST bisects QR.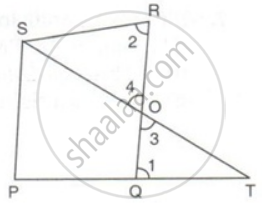
ABCD is a rectangle with ∠ADB = 55°, calculate ∠ABD.
Prove that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides, and is equal to half the difference of these sides.
In the given figure, PQRS is a trapezium in which PQ ‖ SR and PS = QR. Prove that: ∠PSR = ∠QRS and ∠SPQ = ∠RQP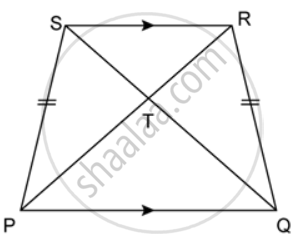
Prove that the diagonals of a kite intersect each other at right angles.
The diagonals AC and BC of a quadrilateral ABCD intersect at O. Prove that if BO = OD, then areas of ΔABC an ΔADC area equal.
In the given figure, AB ∥ SQ ∥ DC and AD ∥ PR ∥ BC. If the area of quadrilateral ABCD is 24 square units, find the area of quadrilateral PQRS.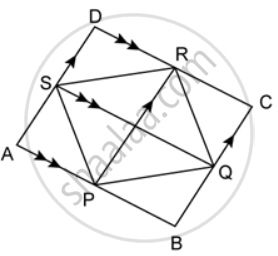
The medians QM and RN of ΔPQR intersect at O. Prove that: area of ΔROQ = area of quadrilateral PMON.
